题目内容

整数数列{an}满足a2=4，2+
1
an+1
＜
1
an
+
1
an+1
1
n
-
1
n+1
＜2+
1
an
，则数列{an}的通项an=
 
．
分析：由题设知
lim
n→∞
（2+
1
an+1
）=2，
lim
n→∞
（2+
1
an
）=2，根据夹逼定理有
lim
n→∞
1
an
+
1
an+1
1
n
-
1
n+1
=2，由此可知an=n2．
解答：解：∵a2=4，2+
1
an+1
＜
1
an
+
1
an+1
1
n
-
1
n+1
＜2+
1
an
，
∴an是递增函数，
∵an是正数列，∴
lim
n→∞
（2+
1
an+1
）=2，
lim
n→∞
（2+
1
an
）=2，
∴根据夹逼定理有
lim
n→∞
1
an
+
1
an+1
1
n
-
1
n+1
=2，
也就是说an必须是n的2次项才能存在极限，且为2，观察数列a2=4，
∴an=n2．
故答案为：n2．
点评：本题考查看数列的递推式，解题时要注意极限的合理运用．
练习册系列答案
相关题目
设正整数数列{an}满足a1=2，a2=6，当n≥2时，有|
a
2
n
-an-1an+1| ＜  
1
2
an-1．
（1）求a3的值；（2）求数列{an}的通项；
（3）记Tn=
12
a1
+
22
a2
+
32
a3
 +K+
n2
an
，证明：对任意n∈N*，Tn＜
9
4
．
已知整数数列{an}满足：a1=1，a2=2，且2an-1＜an-1+an+1＜2an+1（n∈N，n≥2）．
（1）求数列{an}的通项公式；
（2）将数列{an}中的所有项依次按如图所示的规律循环地排成如下三角形数表：
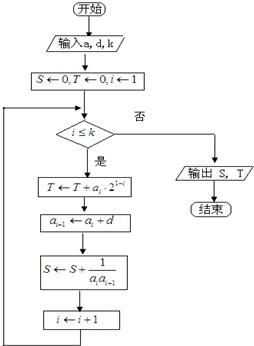精英家教网
…
依次计算各个三角形数表内各行中的各数之和，设由这些和按原来行的前后顺序构成的数列为{bn}，求b5+b100的值；
（3）令cn=2+ban+b•2an-1（b为大于等于3的正整数），问数列{cn}中是否存在连续三项成等比数列？若存在，求出所有成等比数列的连续三项；若不存在，请说明理由．
精英家教网如图所示，流程图给出了无穷整数数列{an}满足的条件，a1∈N+，且当k=5时，输出的S=-
5
9
；当k=10时，输出的S=-
10
99
．
（1）试求数列{an}的通项公式an；
（2）是否存在最小的正数M使得Tn≤M对一切正整数n都成立，若存在，求出M的值；若不存在，请说明理由．
正整数数列{an}满足：a1=1，an+1=
an-n，an＞n
an+n，an≤n.

（Ⅰ）写出数列{an}的前5项；
（Ⅱ）将数列{an}中所有值为1的项的项数按从小到大的顺序依次排列，得到数列{nk}，试用nk表示nk+1（不必证明）；
（Ⅲ）求最小的正整数n，使an=2013．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网