题目内容
f'(x)是f(x)=cosx•esinx的导函数,则f′(x)=________.
(cos2x-sinx)esinx
分析:直接根据两个函数积的导数的求导法则再结合复合函数的求导法则即可求解.
解答:∵f(x)=cosx•esinx
∴f′(x)=(cosx)′esinx+cosx(esinx)′=-sinxesinx+cosxesinxcosx=(cos2x-sinx)esinx
故答案为(cos2x-sinx)esinx
点评:本题主要考察了积的导数和复合函数的导数.解题的关键是熟记积的导数和复合函数的导数公式!
分析:直接根据两个函数积的导数的求导法则再结合复合函数的求导法则即可求解.
解答:∵f(x)=cosx•esinx
∴f′(x)=(cosx)′esinx+cosx(esinx)′=-sinxesinx+cosxesinxcosx=(cos2x-sinx)esinx
故答案为(cos2x-sinx)esinx
点评:本题主要考察了积的导数和复合函数的导数.解题的关键是熟记积的导数和复合函数的导数公式!

练习册系列答案
相关题目
已知点(
,
)在幂函数y=f(x)的图象上,则f(x)的表达式是( )
| ||
| 3 |
| ||
| 9 |
| A、f(x)=3x | ||
| B、f(x)=x3 | ||
| C、f(x)=x-2 | ||
D、f(x)=(
|
 .
.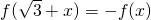 成立,当
成立,当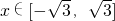 时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤g(a2-a+2)对
时,f(x)=x3-3x.若关于x的不等式g[f(x)]≤g(a2-a+2)对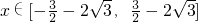 恒成立,则a的取值范围是
恒成立,则a的取值范围是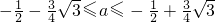 ?
?