题目内容

已知函数f（x）=-x³+ax²-4（a∈R）．若函数y=f（x）的图象在点P（1，f（1））处的切线的倾斜角为 $数学公式$ ．
（1）求a；
（2）设f（x）的导函数是f'（x），若m，n∈[-1，1]，求f（m）+f'（n）的最小值；
（3）对实数m的值，讨论关于x的方程f（x）=m的解的个数．

解：（1）f'（x）=-3x²+2ax．
据题意， $\text{[math]}$
∴-3+2a=1，即a=2…（3分）
（2）由（1）知f（x）=-x³+2x²-4，f'（x）=-3x²+4x．

x	-1	（-1，0）	0	（0，1）	1
f'（x）	-7	-	0	-	1
f（x）	-1		-4		-3

∴对于m∈[-1，1]，f（m）的最小值为f（0）=-4．
∵f'（x）=-3x²-4x的对称轴为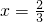 $\text{[math]}$ ，且抛物线开口向下，
∴x∈[-1，1]时，f'（x）最小值为f'（-1）与f'（1）中较小的
∵f'（1）=1，f'（-1）=-7
∴当x∈[-1，1]时，在f'（x）的最小值为-7
∴当x∈[-1，1]时，在f'（n）的最小值为-7
∴f（m）+f'（n）的最小值为-11
（3）求得 $\text{[math]}$ ．
依题意可画出函数y=f（x）草图，得
当 $\text{[math]}$ 或m＜-4时，方程有一解；
当 $\text{[math]}$ 或m=-4时，方程有两解；
当 $\text{[math]}$ 时，方程有三解；

分析：（1）根据函数y=f（x）的图象在点P（1，f（1））处的切线的倾斜角为 $\text{[math]}$ ，利用函数在某点的导数值等于函数图象在该点的切线的斜率，即可求得．
（2）分别计算f（m），f'（n）的最小值．利用导数在某个区间上的符号，确定函数单调性，进而确定函数最值．
（3）先求得 $\text{[math]}$ ．画出函数y=f（x）草图，根据y=f（x）与y=m的交点个数，可确定方程f（x）=m的解的个数．
点评：本题以函数为载体，考查导数的几何意义，考查利用导数解决函数的最值问题，同时考查了数形结合的数学思想，解题的关键是正确利用导数工具．