题目内容
18.已知命题p:x2-3x+2>0;命题q:0<x<a.若p是q的必要而不充分条件,求实数a的取值范围.分析 求解一元二次不等式化简命题P,然后结合p是q的必要而不充分条件求得实数a的取值范围.
解答 解:对于命题p:x2-3x+2>0,解得:x>2或x<1,
∴命题p:x>2或x<1,
又∵命题q:0<x<a,且p是q的必要而不充分条件,
当a≤0时,q:x∈∅,符合题意;
当a>0时,要使p是q的必要而不充分条件,
需{x|0<x<a}?{x|x>2或x<1},
∴0<a≤1.
综上,取并集可得a∈(-∞,1].
点评 本题考查必要条件、充分条件与充要条件的判断方法,考查了一元二次不等式的解法,是基础题.

练习册系列答案
相关题目
13.某学校有高一学生1200人,高二学生1000人,高三学生800人.用分层抽样的方法从中抽取150人,则抽取的高三学生、高二学生、高一学生的人数分别为( )
| A. | 60、50、40 | B. | 50、60、40 | C. | 40、50、60 | D. | 60、40、50 |
3.函数y=tan4x的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
7.随机掷两枚质地均匀的骰子,它们向上的点数之和小于6的概率记为p1,点数之和大于6的概率记为p2,点数之和为偶数的概率记为p3,则( )
| A. | p1<p2<p3 | B. | p1<p3<p2 | C. | p2<p1<p3 | D. | p3<p1<p2 |
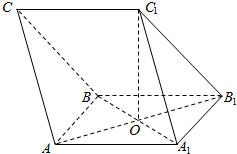 如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.
如图,在三棱柱ABC-A1B1C1中,O是正方形AA1B1B的中心,AB=2$\sqrt{2}$,C1O⊥平面AA1B1B,且C1O=2.