题目内容
如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直.
(1)求证:AB⊥平面BCD;
(2)求点C到平面ABD的距离;
(3)在BD上是否存在一点P,使CP⊥平面ABD,证明你的结论.
(1)求证:AB⊥平面BCD;
(2)求点C到平面ABD的距离;
(3)在BD上是否存在一点P,使CP⊥平面ABD,证明你的结论.

(1)取AC的中点M,因为AB=AC,所以BM⊥AC
∵平面ABC⊥平面ACD,∴BM⊥平面ACD,∴BM⊥CD
∵AB=BC=CD=a,∠B=
∴∠BAC=∠BCA=
∵∠ACD=
,∴∠ACD=
,即AC⊥CD
∵AC∩BM=M∴CD⊥平面ABC∴CD⊥AB
∵AB⊥BC且BC∩CD=C
AB⊥平面BCD
(2)由(1)知BA为B到平面ACD的距离,且BM=
a
设点C到平面ABD的距离h
由已知可得AC=
a,∠ACD=
,由(1)可得∠AMD=
,从而可得AD=
=
a
根据等体积可得
×
×BM×SACD=
×
×SABD×h
∴
×
a×a=a×
a×h
h=
a
点C到平面ABD的距离
a
(3)假设存在满足条件的P,使得CP⊥平面ABD
则CP⊥BD①,∵BC=CD=a∴P为DB的中点
而此时CP=
,AP=
,AC=
a,则AC2=AP2+CP2
∴AP⊥CP②由①②根据直线与平面垂直的判定定理可得此时的P满足条件,
故存在P为BD的中点
∵平面ABC⊥平面ACD,∴BM⊥平面ACD,∴BM⊥CD
∵AB=BC=CD=a,∠B=
| π |
| 2 |
| π |
| 4 |
∵∠ACD=
| 3π |
| 4 |
| π |
| 2 |
∵AC∩BM=M∴CD⊥平面ABC∴CD⊥AB
∵AB⊥BC且BC∩CD=C
AB⊥平面BCD
(2)由(1)知BA为B到平面ACD的距离,且BM=
| ||
| 2 |
设点C到平面ABD的距离h
由已知可得AC=
| 2 |
| π |
| 2 |
| π |
| 2 |
| AM2+ DM2 |
| 2 |
根据等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴
| ||
| 2 |
| 2 |
| 2 |
h=
| ||
| 2 |
点C到平面ABD的距离
| ||
| 2 |
(3)假设存在满足条件的P,使得CP⊥平面ABD
则CP⊥BD①,∵BC=CD=a∴P为DB的中点
而此时CP=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴AP⊥CP②由①②根据直线与平面垂直的判定定理可得此时的P满足条件,
故存在P为BD的中点

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
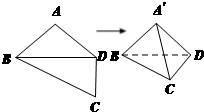 如图,平面四边形ABCD中,AB=AD=CD=1,BD=
如图,平面四边形ABCD中,AB=AD=CD=1,BD=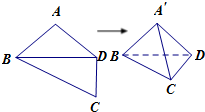 如图,平面四边形ABCD中,AB=AD=CD=1,
如图,平面四边形ABCD中,AB=AD=CD=1, 如图,平面四边形ABCD中,AB=13,AC=10,AD=5,
如图,平面四边形ABCD中,AB=13,AC=10,AD=5, 如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,
如图:平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠BCD=135°,沿对角线AC将△ADC折起,使面ADC⊥面ABC,