题目内容
10．求到两不同定点距离之比为一常数λ（λ≠0）的动点的轨迹．分析 设点M（x，y）是曲线上的任意一点，欲求出动点M的轨迹方程，只须求出x，y的关系式即可，结合距离的比，用坐标来表示距离，利用两点间的距离公式化简即可求得点P的轨迹方程．
解答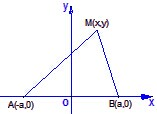 
解：建立坐标系如图所示，设|AB|=2a，则A（-a，0），B（a，0）．设M（x，y）是轨迹上任意一点．
则由题设，得$\frac{|MA|}{|MB|}$=λ，坐标代入，得$\frac{\sqrt{（x+a）^{2}+{y}^{2}}}{\sqrt{（x-a）^{2}+{y}^{2}}}$=λ，
化简得（1-λ2）x2+（1-λ2）y2+2a（1+λ2）x+（1-λ2）a2=0
（1）当λ=1时，即|MA|=|MB|时，点M的轨迹方程是x=0，点M的轨迹是直线（y轴）．
（2）当λ≠1且λ≠0时，点M的轨迹方程是x2+y2+$\frac{2a（1+{λ}^{2}）}{1-{λ}^{2}}$x+a2=0，点M的轨迹是以（-$\frac{a（1+{λ}^{2}）}{1-{λ}^{2}}$，0）为圆心，$\frac{2aλ}{|1-{λ}^{2}|}$为半径的圆．
点评 本题考查轨迹方程，利用的是直接法，直接法是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程．
练习册系列答案
相关题目
