Question

如图所示，已知椭圆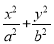＝1(a＞b＞0)的右焦点为F2(1,0)，点A在椭圆上．

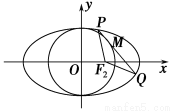
(1)求椭圆方程；

(2)点M(x0，y0)在圆x2＋y2＝b2上，点M在第一象限，过点M作圆x2＋y2＝b2的切线交椭圆于P、Q两点，问|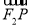|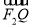＋||＋||是否为定值？如果是，求出该定值；如果不是，说明理由．

 

Answer 1

（1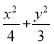）＝1（2）4

【解析】(1)由右焦点为F2(1,0)，可知c＝1.设左焦点为F1，则F1(－1,0)，又点A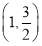在椭圆上，则

2a＝|AF1|＋|AF2|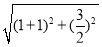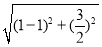＝＋＝4，

∴a＝2，b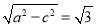＝，即椭圆方程为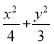＝1；

(2)设P(x1，y1)，Q(x2，y2)，则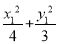＝1(|x1|≤2)，

|PF2|2＝(x1－1)2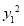＋＝(x1－1)2＋3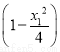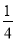＝(x1－4)2，

∴|PF2|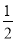＝(4－x1)＝2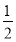－x1.

连结OM，OP，由相切条件知：

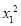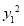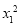|PM|2＝|OP|2－|OM|2＝＋－3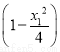＝＋3－3＝，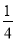

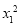显然x1＞0，∴|PM|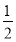＝x1.

∴|PF2|＋|PM|＝2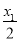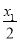－＋＝2.同理|QF2|＋|QM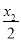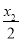|＝2－＋＝2.

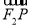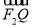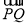∴||＋||＋||＝2＋2＝4为定值．