题目内容
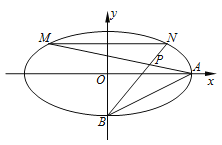
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的右、下顶点,且
的右、下顶点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
, ![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
, ![]() .
.
(i) 若![]() ,
, ![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
(ii) 求证: ![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
【答案】(1)![]() . (2)(i)
. (2)(i) ![]() ;(ii) 见解析.
;(ii) 见解析.
【解析】试题分析:
(1)由题意求得![]() ,椭圆的方程为
,椭圆的方程为![]() .
.
(2)(i)设出点的坐标和直线方程,联立直线与椭圆的方程,得到关于实数k的方程,解方程可得![]() ;
;
(ii)利用题意证得![]() ,则
,则![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.
试题解析:
(1)由![]() 知,
知, ![]() ,
,
又椭圆![]() 过点
过点![]() ,所以
,所以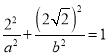 ,
,
解得![]() 所以椭圆
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
联立![]() 消去
消去![]() 并整理得,
并整理得, ![]() ,
,
解得![]() ,
, ![]() ,所以
,所以 .
.
因为直线![]() ,
, ![]() 的斜率乘积为
的斜率乘积为![]() ,所以直线
,所以直线![]() 的方程
的方程![]() .
.
联立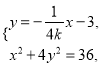 消去
消去![]() 并整理得,
并整理得, ![]() ,
,
解得![]() ,
, ![]() ,所以
,所以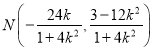 .
.
(i) 因为![]() ,
, ![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
当![]() 时,点
时,点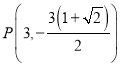 在椭圆
在椭圆![]() 外,不满足题意.
外,不满足题意.
所以直线![]() 的斜率为
的斜率为![]() .
.
(ii) 联立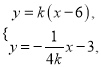 解得
解得![]() .
.
所以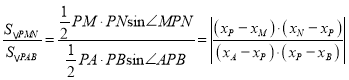
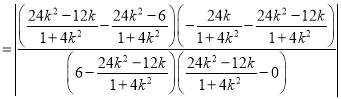
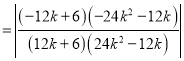
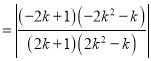
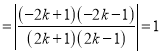 .
.
故![]() 的面积与
的面积与![]() 的面积相等.
的面积相等.

【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况,从该市当天参与网购的顾客中随机抽查了男女各30人,统计其网购金额,得到如下频率分布直方图:

网购达人 | 非网购达人 | 合计 | |
男性 | 30 | ||
女性 | 12 | 30 | |
合计 | 60 |
若网购金额超过![]() 千元的顾客称为“网购达人”,网购金额不超过
千元的顾客称为“网购达人”,网购金额不超过![]() 千元的顾客称为“非网购达人”.
千元的顾客称为“非网购达人”.
(Ⅰ)若抽取的“网购达人”中女性占12人,请根据条件完成上面的![]() 列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
列联表,并判断是否有99%的把握认为“网购达人”与性别有关?
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定12人,若需从这12人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考公式:  ,其中
,其中![]() )
)
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |