题目内容
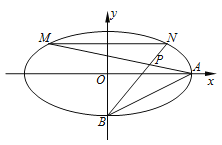
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过右焦点
,过右焦点![]() 垂直于
垂直于![]() 轴的直线与椭圆交于
轴的直线与椭圆交于![]() ,
, ![]() 两点且
两点且![]() ,又过左焦点
,又过左焦点![]() 任作直线
任作直线![]() 交椭圆于点
交椭圆于点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆![]() 上两点
上两点![]() ,
, ![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:
(1)由题意求得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线斜率存在且![]() 时,联立直线与椭圆的方程计算可得假设 不成立;
时,联立直线与椭圆的方程计算可得假设 不成立;
当直线的斜率![]() 时,面积函数
时,面积函数![]() ,结合椭圆方程和均值不等式的结论可得
,结合椭圆方程和均值不等式的结论可得![]() 面积的最大值为
面积的最大值为![]() .
.
试题解析:
(Ⅰ)由条件有![]() ,∴
,∴![]() ,又
,又![]() ,且
,且![]() ,
,
∴![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)依题意直线![]() 不垂直
不垂直![]() 轴,当直线
轴,当直线![]() 的斜率
的斜率![]() 时,可设直线
时,可设直线![]() 的方程为
的方程为![]() (
(![]() ),则直线
),则直线![]() 的方程为
的方程为![]() .
.
由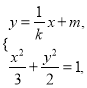 得
得![]() ,
,
![]() ,即
,即![]() ,①
,①
设![]() 的中点为
的中点为![]() ,则
,则![]() ,
, ![]() ,
,
点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,故
,故![]() ,②
,②
此时![]() 与①矛盾,故
与①矛盾,故![]() 时不成立.
时不成立.
当直线![]() 的斜率
的斜率![]() 时,
时, ![]() ,
, ![]() (
(![]() ,
, ![]() ),
),
![]() 的面积
的面积![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 面积的最大值为
面积的最大值为![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.

练习册系列答案
相关题目