题目内容
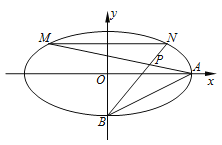
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点F且垂直于x轴的直线与椭圆
,过左焦点F且垂直于x轴的直线与椭圆![]() 相交,所得弦长为1,斜率为
相交,所得弦长为1,斜率为![]() (
(![]() )的直线
)的直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得无论
,使得无论![]() 取何值,
取何值, ![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)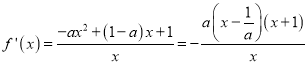 (2)存在点M(2,0)满足题意,且常数为0.
(2)存在点M(2,0)满足题意,且常数为0.
【解析】试题分析:(I)由题意可知得![]() 的值,即可求解椭圆的标准方程;
的值,即可求解椭圆的标准方程;
(II)设在![]() 轴上存在点
轴上存在点![]() 满足题意,设直线
满足题意,设直线![]() 的方程可设为
的方程可设为![]() 与椭圆的方程联立方程组,得出
与椭圆的方程联立方程组,得出![]() 和
和![]() ,利用
,利用![]() ,求得
,求得![]() ,即可确定结论.
,即可确定结论.
试题解析:(I)由题意可知椭圆![]() 过点
过点![]() ,则
,则![]() ,
,
又![]()
解得![]() ,则椭圆方程
,则椭圆方程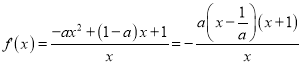 .
.
(II)设在x轴上存在点M(t,0)满足题意,
![]() 直线
直线![]() 过点(1, 0)且斜率为k,则直线
过点(1, 0)且斜率为k,则直线![]() 的方程可设为:
的方程可设为: ![]()
由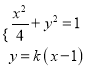 可知:
可知: ![]()
![]()
易知: ![]() 设
设 ![]()
则: 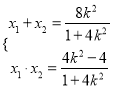
![]()
由题可设: ![]()
![]() 对任意实数
对任意实数![]() 恒成立;
恒成立;
![]() 解得:
解得: ![]()
存在点M(2,0)满足题意,且常数为0.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目