题目内容
7.正项数列{an}的前n项和为Sn,满足an2+3an=6Sn+4(1)求{an}的通项公式
(2)设bn=2nan,求数列{bn}的前n项和Tn.
分析 (1)将n换为n+1,相减,分解因式,结合条件可得an+1-an=3,再由等差数列的通项公式即可得到所求;
(2)求得${b_n}={2^n}{a_n}=(3n+1)•{2^n}$,再由数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
解答 解:(1)由$a_n^2+3{a_n}=6{S_n}+4$…①,
可得$a_{n+1}^2+3{a_{n+1}}=6{S_{n+1}}+4$…②,
由②-①得$a_{n+1}^2-a_n^2+3{a_{n+1}}-3{a_n}=6{S_{n+1}}-6{S_n}=6{a_{n+1}}$,
即(an+1+an)(an+1-an-3)=0,
∵an>0,∴an+1+an>0,∴an+1-an-3=0,
即an+1-an=3,
又$a_1^2+3{a_1}=6{S_1}+4=6{a_1}+4$,
即$a_1^2-3{a_1}-4=({a_1}-4)({a_1}+1)=0$,
∵an>0,∴a1=4,
∴{an}是4为首项,3为公差的等差数列,
∴an=4+3(n-1)=3n+1;
(2)${b_n}={2^n}{a_n}=(3n+1)•{2^n}$,
故${T_n}=4•{2^1}+7•{2^2}+10•{2^3}+…+(3n+1)•{2^n}$,
$2{T_n}=\;4•{2^2}+7•{2^3}+10•{2^4}+…+(3n+1)•{2^{n+1}}$,
两式相减可得-Tn=8+3(4+8+…+2n)-(3n+1)•2n+1,
=2+3(2+4+8+…+2n)-(3n+1)•2n+1
=${2^1}+3•\frac{{2({2^n}-1)}}{2-1}-(3n+1)•{2^{n+1}}$
=-(3n-2)•2n+1-4,
∴${T_n}=(3n-2)•{2^{n+1}}+4$.
点评 本题考查数列的通项公式的求法,注意运用下标相减和等差数列的通项公式,考查数列的求和方法:错位相减法,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 5 | C. | 2 | D. | 1 |
| A. | 若x≥0,则2x≤3x | B. | 若x>0,则 2x<3x | C. | 若2x>3x,则x≥0 | D. | 若2x≤3x,则x>0 |
| A. | $({1,\sqrt{2}}]$ | B. | $({0,\sqrt{2}}]$ | C. | $[{\sqrt{2},2})$ | D. | $[{\sqrt{2},\sqrt{3}}]$ |
| A. | (-∞,1] | B. | [1,+∞) | C. | (0,1] | D. | (0,+∞) |
| A. | (-2,5) | B. | (-2,-5) | C. | (2,-5) | D. | (2,5) |
 据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).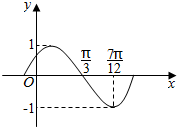 函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=sin(ωx+φ)(ω>0,|φ|>$\frac{π}{2}$)的部分图象如图所示.