题目内容
函数![]()
![]() .
.
(I)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,求实数
,求实数![]() 的值;
的值;
(II)若![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的单调区间.
的单调区间.
(1)a =1 (2)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
解析:
(I)![]() , ………3分
, ………3分
若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
则 ![]() . ……5分
. ……5分
所以,![]() ,得 a =1. ……6分
,得 a =1. ……6分
(II) 因为![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() , ………………7分
, ………………7分
即![]() ,
,![]() , …………………8分
, …………………8分
![]() . …………………9分
. …………………9分
因为![]() 的定义域为
的定义域为![]() ,所以有:
,所以有:
|
|
|
|
|
| 1 |
|
|
| + | 0 |
|
| 0 | + |
|
| 增 | 极大值 | 减 | 减 | 极小值 | 增 |
………11分
所以,![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .…13分
.…13分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,求
,求 在
在 处的切线方程;(II)求
处的切线方程;(II)求 上的最小值.
上的最小值. .
.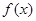 在
在 [1,+∞
[1,+∞ 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;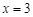 是
是 .
. 在
在 [1,+∞
[1,+∞ 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围; 是
是