题目内容
在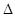 ABC中,
ABC中,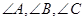 所对的边分别为a,b,c,已知a=2,b=
所对的边分别为a,b,c,已知a=2,b=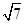 ,
,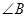 =
= ,则
,则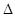 ABC的面积为
ABC的面积为
A.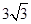 | B.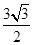 | C. | D.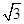 |
B
解析试题分析:根据题意已知两边以及一边的对角,则利用中正弦定理来得到A,然后结合余弦定理得到C,再次运用正弦面积公式得到结论。
因为a=2,b=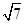 ,
,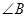 =
= ,则有正弦定理可知
,则有正弦定理可知 ,那么可知A<B,sinC="sin(A+B)="
,那么可知A<B,sinC="sin(A+B)="  ,而三角形的面积公式为
,而三角形的面积公式为 ,故选B.
,故选B.
考点:三角形面积的求解
点评:解决该试题的关键是通过变角的给定确定出运用正弦定理先求角A,然后得到角C,进而结合面积公式得到,属于基础题。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
在 中,内角
中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 的值为( )
的值为( )
| A.30° | B.60° | C.120° | D.150° |
在△ABC中,内角 的对边分别是
的对边分别是 ,若
,若 ,
, ,则
,则 )
)
A. | B. | C. | D. |
在△ABC中,若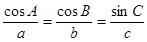 ,则△ABC是( )
,则△ABC是( )
| A.有一内角为30°的直角三角形 | B.等腰直角三角形 |
| C.有一内角为30°的等腰三角形 | D.等边三角形 |
在△ABC中,A=60°,b=1,其面积为 ,则
,则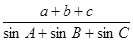 等于( )
等于( )
A.3 | B.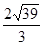 |
C.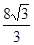 | D.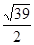 |
若∆ABC的三个内角成等差数列,三边成等比数列,则∆ABC是
| A.直角三角形 | B.等腰直角三角形 | C.等边三角形 | D.钝角三角形 |
在△ 中,角
中,角 所对的边分别为
所对的边分别为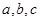 ,且满足
,且满足 ,则
,则 的最大值是( )
的最大值是( )
A. | B.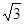 | C. | D.2 |
 的取值范围是
的取值范围是 ) C.(1,
) C.(1,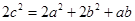 ,则△ABC是( )
,则△ABC是( )