题目内容
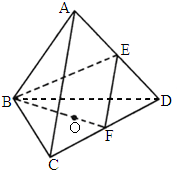
如下图，点O是正△ABC平面外一点，若OA=OB=OC=AB=1，E、F分别是AB、OC的中点，试求OE与BF夹角的余弦.
解：设
=a,
=b,
=c,则a·b=b·c=c·a=
,|a|=|b|=|c|=1,
·
=
（a+b）·(
c-b)=
(
a·c+
b·c-a·b-|b|2)=
×(
+
-
-1)=-
,
∴cos〈
,
〉=
=
.
∴OE与BF所成角的余弦为
.
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
相关题目
,则球O的表面积是（ ）
,
),△AOB为正三角形,则 