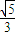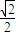题目内容
如图,点F(-c,0)为双曲线C: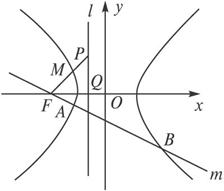
(1)求双曲线C的标准方程;
(2)若过点F的直线m与双曲线C的左右两支分别交于A、B两点,设![]() =λ
=λ![]() ,当λ∈[6,+∞)时,求直线m的斜率k的取值范围.
,当λ∈[6,+∞)时,求直线m的斜率k的取值范围.
解:(1)由c2=a2+b2,①|FQ|=c![]() =1,∴b2=c.②
=1,∴b2=c.②
由中点坐标公式得M(-c+![]() 2,
2,![]() ).
).
又M(-c+![]() ,
,![]() )在双曲线上,∴
)在双曲线上,∴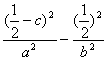 =1.③
=1.③
联立①②③,解得a=b=2,c=2.∴双曲线方程为x2-y2=2.
(2)由(1),F(-2,0),设A(x1,y1),B(x2,y2),直线m:y=k(x+2),则由![]() =λ
=λ![]() ,得x2=λ(x1+2)-2,y2=λy1.由
,得x2=λ(x1+2)-2,y2=λy1.由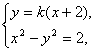 得(1-k2)y2-4ky+2k2=0.
得(1-k2)y2-4ky+2k2=0.
Δ=16k2-8k2(1-k2)=8k2(1+k2).∴y1+y2=![]() ,y1y2=
,y1y2=![]() .7分
.7分
由y2=λy1,y1+y2=![]() ,y1y2=
,y1y2=![]() ,消去y1,y2,
,消去y1,y2,
得![]() =
=![]() =λ+
=λ+![]() +2.
+2.
∵λ≥6,函数g(λ)=λ+![]() +2在(1,+∞)上单调递增,∴
+2在(1,+∞)上单调递增,∴![]() ≥6+
≥6+![]() +2=
+2=![]() .∴k2≥
.∴k2≥![]() .
.
又直线m与双曲线的两支相交,即方程(1-k2)y2-4ky+2k2=0两根同号,
∴k2<1.∴![]() ≤k2<1.故k∈(-1,
≤k2<1.故k∈(-1,![]() ]∪[
]∪[![]() ,1).
,1).

练习册系列答案
相关题目
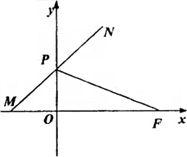 如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且
如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且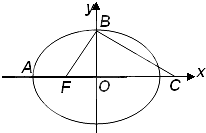 (2009•泰安一模)如图,点F是椭圆
(2009•泰安一模)如图,点F是椭圆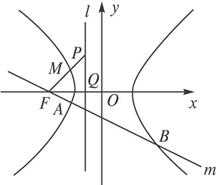
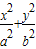 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )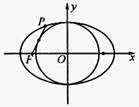

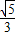
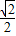

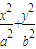 =1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
=1(a>b>0)的一个焦点,若椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )