题目内容
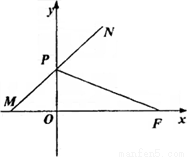
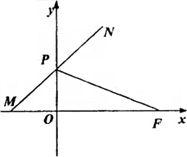 如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且
如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且| PM |
| PF |
| PN |
| PM |
| 0 |
(1)求点N的轨迹C;
(2)过点F(a,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设K(-a,0),
| KA |
| KB |
| π |
| 2 |
分析:(1)先设点N(x,y),然后可以得到向量
、
,进而根据
+
=
、
•
=0可得答案.
(2)先设出直线方程,然后和(1)中所求的轨迹方程联立得到两根之和与两根之积,进而由
•
>0得到答案.
| PM |
| PF |
| PN |
| PM |
| 0 |
| PM |
| PF |
(2)先设出直线方程,然后和(1)中所求的轨迹方程联立得到两根之和与两根之积,进而由
| KA |
| KB |
解答:解:(1)设N(x,y)∵
+
=
∴M(-x,0),P(0,
)
=(-X,-
),
=(a,-
)
∵
•
=0∴
•
=-ax+
=0
∴y2=4ax
(2)设A(x1,y1),B(x2,y2)
∴直线l:y=k(x-a)
=(x1+a,y1)
=(x2+a,y2)
联立
∴ky2-4ay-4ka2=0
∴y1+y2=
,y1y2=-4a2,x1x2=a2,x1+x2=
∴
•
=(x1+a)(x2+a)+y1y2=x1x2+a(x1+x2)+a2+y1y2
=2a2+
-4a2=
-2a2=2a2(1+
-1)=
>0
∴cosθ>0∵θ∈[0,π]∴θ∈(0,
)
| PN |
| PM |
| 0 |
∴M(-x,0),P(0,
| y |
| 2 |
| PM |
| y |
| 2 |
| PF |
| y |
| 2 |
∵
| PM |
| PF |
| PM |
| PF |
| y2 |
| 4 |
∴y2=4ax
(2)设A(x1,y1),B(x2,y2)
∴直线l:y=k(x-a)
| KA |
| KB |
联立
|
∴y1+y2=
| 4a |
| k |
| 2a(k2+2) |
| k2 |
∴
| KA |
| KB |
=2a2+
| 2a2(k2+2) |
| k2 |
| 2a2(k2+2) |
| k2 |
| 2 |
| k2 |
| 4a2 |
| k2 |
∴cosθ>0∵θ∈[0,π]∴θ∈(0,
| π |
| 2 |
点评:本题主要考查向量的数量积运算和圆锥曲线的有关问题.在解决圆锥曲线的有关问题时,一般都是联立直线方程和圆锥曲线方程求出两根之和与两根之积,然后 根据题意解题.

练习册系列答案
相关题目
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点( 如图,点F是椭圆W:
如图,点F是椭圆W: 如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且
如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且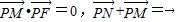 .
.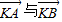 的夹角为θ,求证
的夹角为θ,求证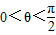 .
. 如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且
如图,点F(a,0)(a>0),点P在y轴上运动,点M在x轴上运动,点N为动点,且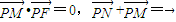 .
.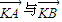 的夹角为θ,求证
的夹角为θ,求证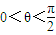 .
.