题目内容
7.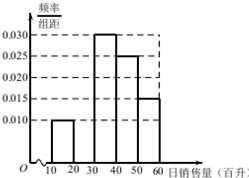 某加油站20名员工日销售量的频率分布直方图,如图所示:
某加油站20名员工日销售量的频率分布直方图,如图所示:(Ⅰ)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在[10,20),[20,30)的员工数;
(Ⅱ)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在[20,30)的概率.
分析 (Ⅰ)先求出日销售量在[20,30)的频率,从而能求出销售量在[20,30)的小矩形高度,进而能求出频率分布图,由此能求出日销售量在[10,20)的员工数和日销售量在[20,30)的员工数.
(Ⅱ)由(Ⅰ)知日销售量在[10,30)的员工共有6人,在[10,20)的员工共有2人,在[20,30)的员工有4人,由此利用等可能事件概率计算公式能求出这两名员工日销量在[20,30)的概率.
解答 解:(Ⅰ)日销售量在[20,30)的频率为1-10×(0.010+0.030+0.025+0.015)=0.2,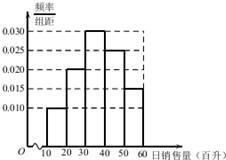
故销售量在[20,30)的小矩形高度为$\frac{0.2}{10}$=0.02,
∴频率分布图如右图所示:
日销售量在[10,20)的员工数为:20×10×0.010=2,
日销售量在[20,30)的员工数为:20×10×0.020=4.
(Ⅱ)由(Ⅰ)知日销售量在[10,30)的员工共有6人,在[10,20)的员工共有2人,在[20,30)的员工有4人,
从此6人中随机抽2人,基本事件总数n=${C}_{6}^{2}$=15,
这2名员工日销售量在[20,30)包含的基本事件个数m=${C}_{4}^{2}=6$,
∴这两名员工日销量在[20,30)的概率p=$\frac{m}{n}=\frac{6}{15}=\frac{2}{5}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
17.若0<b<a<1则下列结论不一定成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | $\sqrt{a}$>$\sqrt{b}$ | C. | ab>ba | D. | logba>logab |
15.设a>0且a≠1,b∈R,则“a>1,0<b<1”是“函数y=loga(x+b),(x>-b)的图象同时经过第一、三、四象限”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.函数y=$\frac{1}{x}$+$\sqrt{x+4}$的定义域为( )
| A. | [-4,+∞) | B. | (-4,0)∪(0,+∞) | C. | (-4,+∞) | D. | [-4,0)∪(0,+∞) |