Question

（08年黄冈市模拟理） （12分）在五棱锥P―ABCDE中，PA＝AB＝AE＝2a, PB=PE=2a, BC=DE=a, ∠EAB=∠ABC=∠DEA=90°.

(1)求证：PA平面ABCDE;

(2)求二面角A―PD―C的大小;

(3)在线段BC上是否存在一点Q，使Q到平面PDE的距离为.

 

Answer 1

解析：（1）由PA⊥AE，PA⊥AB得PA⊥平面ABCD    ……4分

（2）过C作CM⊥AD，MN⊥PD于N，连CN，则∠CNM为二面角A―PD―C的一个平面角，……5分

CD＝，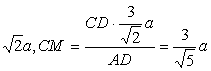

,所求二面角的大小为……8分

（3）假设存在Q点，过Q作QF∥AB交AE于F，由ED∥AB得QF∥平面PDE，

由DE⊥平面PAE，所以平面PAE⊥平面PED，作FH⊥PE交PE于H，则FH⊥平

面PED，在Rt△EFH中，FH＝，∠FEH＝45°,所以FE＝,所以Q是

BC中点…………12分

解法二（2）建立如图坐标系，设A(0,0,0),P(0,0,2a),D(a,2a,0),C(2a,a,0),

E(0,2a,0)，设平面PAD的法向量为,

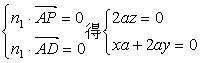所以，

同理平面PDC的法向量，

故所求二面角的大小为

（3）,，可求得平面PDE的法向量

设Q(2a,x,0)点Q到平面PED距离为d,

则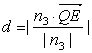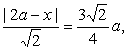＝得，由0<x<a得

即Q为BC中点