题目内容
设x、y∈R,在直角坐标平面内,| a |
| 3 |
| b |
| 3 |
| a |
| b |
(Ⅰ)求C的方程;
(Ⅱ)设直线y=kx+1与C交于A、B两点,k为何值时
| OA |
| OB |
| AB |
分析:(Ⅰ)根据|
|+|
|=4,可判断曲线C为椭圆,欲求 轨迹C的方程,只需求出椭圆的长半轴长,短半轴长,由
=(x,y+
),
=(x,y-
),|
|+|
|=4求出a,b即可.
(Ⅱ)设A(x1,y1)、B(x2,y2),则A,B两点为直线y=kx+1与椭圆交点,可用两曲线方程联立,求x1x2+y1y2,再根据
⊥
时,x1x2+y1y2=0,就可求出k只,再用弦长公式求|
|.
| a |
| b |
| a |
| 3 |
| b |
| 3 |
| a |
| b |
(Ⅱ)设A(x1,y1)、B(x2,y2),则A,B两点为直线y=kx+1与椭圆交点,可用两曲线方程联立,求x1x2+y1y2,再根据
| OA |
| OB |
| AB |
解答:解:(Ⅰ)∵|
|+|
|=4,
∴
+
=4,
它表示以点F1(0,-
、F2(0,
的椭圆,其方程为x2+
=1,这就是所求C的方程.
(Ⅱ设直线y=kx+1与C交于A(x1,y1)、B(x2,y2)两点,
由
消去y得4x2+(kx+1)2=4,整理得(4+k2)x2+2kx-3=0
其△=(2k)2+12(4+k2)>0恒成立.
由韦达定理得x1+x2=-
,x1x2=-
.
则y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=-
-
+1=
,
|x1-x2|=
=
由
⊥
得,x1x2+y1y2=0,即-
+
=0,
解得k=±
,
此时|
|=
|x1-x2|=
.
.综上得,当k=±
时,
⊥
,此时|
|的值是
.
| a |
| b |
∴
x2+(y+
|
x2+(y-
|
它表示以点F1(0,-
| 3) |
| 3) |
| y2 |
| 4 |
(Ⅱ设直线y=kx+1与C交于A(x1,y1)、B(x2,y2)两点,
由
|
其△=(2k)2+12(4+k2)>0恒成立.
由韦达定理得x1+x2=-
| 2k |
| 4+k2 |
| 3 |
| 4+k2 |
则y1y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1=-
| 3k2 |
| 4+k2 |
| 2k2 |
| 4+k2 |
| 4-4k2 |
| 4+k2 |
|x1-x2|=
| (x1+x2)2-4x1x2 |
4
| ||
| 4+k2 |
由
| OA |
| OB |
| 3 |
| 4+k2 |
| 4-4k2 |
| 4+k2 |
解得k=±
| 1 |
| 2 |
此时|
| AB |
| 1+k2 |
4
| ||
| 17 |
.综上得,当k=±
| 1 |
| 2 |
| OA |
| OB |
| AB |
4
| ||
| 17 |
点评:本题考查了定义法求椭圆方程,以及只限于椭圆位置关系的判断,注意设而不求思想的应用.

练习册系列答案
相关题目
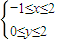 所表示的平面区域是W,从区域W中随机取点M(x,y).
所表示的平面区域是W,从区域W中随机取点M(x,y).