题目内容
如图，若M是抛物线y2=8x上一点，F是抛物线的焦点，以Fx为始边，以FM为终边的角∠xFM=60°，则|FM|的长为（ ）| A、8 | B、4 | C、2 | D、1 |
分析：由题意得MF|=2|FA|即|FM|=2（a-2）且|MF|=
联立可得a=6，进而由抛物线的定义得到|FM|的长为8．
| 2|b| | ||
|
解答：解：由题意得F（2，0）
设点M为（a，b）过点M作MA垂直于x轴，垂直为A
∴|MF|=2|FA|即|FM|=2（a-2）
|MF|=
即|MF|=
所以2（a-2）=
整理得b2=3（a-2）2…①
又∵M是抛物线y2=8x上一点
∴b2=8a…②
有①②可得a=6或a=
（舍去）
所以|MF|=2（6-2）=8
所以|FM|的长为8．
设点M为（a，b）过点M作MA垂直于x轴，垂直为A
∴|MF|=2|FA|即|FM|=2（a-2
）|MF|=
| 2|MA| | ||
|
| 2|b| | ||
|
所以2（a-2）=
| 2|b| | ||
|
又∵M是抛物线y2=8x上一点
∴b2=8a…②
有①②可得a=6或a=
| 2 |
| 3 |
所以|MF|=2（6-2）=8
所以|FM|的长为8．
点评：解决此类问题关键是灵活运用抛物线的定义，将问题转化为我们熟悉的平面几何知识．
练习册系列答案
阅读快车系列答案
相关题目
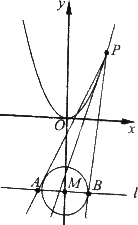
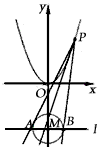
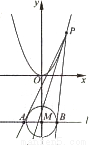
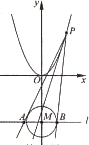如图，设P是抛物线C1：x2=y上的动点．过点P做圆C2：x2+（y+3）2=1的两条切线，交直线l：y=-3于A，B两点．
