题目内容
如图,设P是抛物线C1:x2=y上的动点.过点P做圆C2:x2+(y+3)2=1的两条切线,交直线l:y=-3于A,B两点。
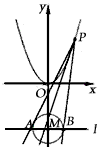
(1)求C2的圆心M到抛物线C1准线的距离;
(2)是否存在点P,使线段AB被抛物线C1在点P处的切线平分?若存在,求出点P的坐标;若不存在,请说明理由。
(2)是否存在点P,使线段AB被抛物线C1在点P处的切线平分?若存在,求出点P的坐标;若不存在,请说明理由。
解:(1)由题意可知,抛物线C1的准线方程为:
所以圆心M到抛物线C1准线的距离为 ;
;
(2)设点P的坐标为(x0,x02),抛物线C1在点P处的切线交直线l于点D
再设A,B,D的横坐标分别为
过点P(x0,x02)的抛物线C1的切线方程为: (1)
(1)
当 时,过点P(1,1)与圆C2的切线PA为:
时,过点P(1,1)与圆C2的切线PA为:
可得
所以
设切线PA,PB的斜率为 ,则
,则
 (2)
(2)
 (3)
(3)
将 分别代入(1),(2),(3),得
分别代入(1),(2),(3),得

从而
又
即
同理
所以 是方程
是方程 的两个不相等的根,从而
的两个不相等的根,从而
 ,
,
因为
所以 ,即
,即
从而
进而得
综上所述,存在点P满足题意,点P的坐标为( ,
, )。
)。

所以圆心M到抛物线C1准线的距离为
 ;
;(2)设点P的坐标为(x0,x02),抛物线C1在点P处的切线交直线l于点D
再设A,B,D的横坐标分别为

过点P(x0,x02)的抛物线C1的切线方程为:
 (1)
(1)当
 时,过点P(1,1)与圆C2的切线PA为:
时,过点P(1,1)与圆C2的切线PA为:
可得

所以

设切线PA,PB的斜率为
 ,则
,则 (2)
(2) (3)
(3)将
 分别代入(1),(2),(3),得
分别代入(1),(2),(3),得
从而

又

即

同理

所以
 是方程
是方程 的两个不相等的根,从而
的两个不相等的根,从而  ,
,
因为

所以
 ,即
,即
从而

进而得

综上所述,存在点P满足题意,点P的坐标为(
 ,
, )。
)。
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
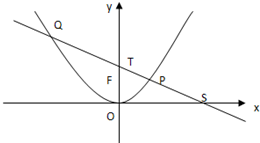 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2). 如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
如图,斜率为1的直线过抛物线Ω:y2=2px(p>0)的焦点F,与抛物线交于两点A,B,
 过抛物线
过抛物线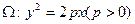 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。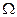 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;
 过抛物线
过抛物线 的焦点F,与抛物线交于两点A,B。
的焦点F,与抛物线交于两点A,B。 的方程;
的方程; 的面积S的最大值;
的面积S的最大值;