题目内容
已知α,β∈(
,π),sinα=
,cosβ=-
,求cos(α+β),tan(2α+
).
| π |
| 2 |
| 3 |
| 5 |
| 5 |
| 13 |
| π |
| 4 |
分析:由已知可求cosα,sinβ,利用tanα=
可求tanα,然后由cos(α+β)=cosαcosβ-sinαsinβ,tan2α=
可求
| sinα |
| cosα |
| 2tanα |
| 1-tan2α |
解答:解:∵α,β∈(
,π),sinα=
,cosβ=-
,
∴cosα=-
,sinβ=
∴tanα=
=-
∴cos(α+β)=cosαcosβ-sinαsinβ
=-
×(-
)-
×
=-
∴tan2α=
=-
tan(2α+
)=
=
=-
| π |
| 2 |
| 3 |
| 5 |
| 5 |
| 13 |
∴cosα=-
| 4 |
| 5 |
| 12 |
| 13 |
∴tanα=
| sinα |
| cosα |
| 3 |
| 4 |
∴cos(α+β)=cosαcosβ-sinαsinβ
=-
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
| -16 |
| 65 |
∴tan2α=
| 2tanα |
| 1-tan2α |
| 24 |
| 7 |
tan(2α+
| π |
| 4 |
| tan2α+1 |
| 1-tan2α |
1-
| ||
1+
|
| -17 |
| 31 |
点评:本题主要考查了同角基本关系的应用,两角和的余弦公式及二倍角的正切公式、两角和的正切公式等公式的综合应用

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 已知定点A
已知定点A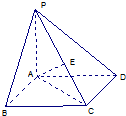 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,