题目内容
（理）已知命题α：2≤x，命题β：|x-m|≤1，且命题α是β的必要条件，求实数m的取值范围．
分析：求出命题β的等价条件，利用命题α是β的必要条件，即可求出m的取值范围．
解答：解：∵|x-m|≤1，
∴m-1≤x≤m+1，
即β：m-1≤x≤m+1，
∵α是β的必要条件，
∴m-1≥2，
即m≥3．
∴m-1≤x≤m+1，
即β：m-1≤x≤m+1，
∵α是β的必要条件，
∴m-1≥2，
即m≥3．
点评：本题主要考查充分条件和必要条件的应用，利用绝对值不等式的解法求出等价条件是解决本题的关键．
练习册系列答案
相关题目
，
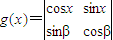，α，β是参数，x∈R，
，
，判别h（x）=f（x）+g（x）的奇偶性；
，判别h（x）=f2（x）+g2（x）的奇偶性；
，t（x）=f（x）g（x）是偶函数，求β；