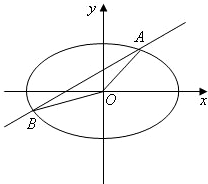
题目内容
如图，直线y=kx+b与椭圆
=1交于A、B两点，记△AOB的面积为S，
（Ⅰ）求在k=0，0＜b＜1的条件下，S的最大值；
（Ⅱ）当|AB|=2，S=1时，求直线AB的方程。
=1交于A、B两点，记△AOB的面积为S， （Ⅰ）求在k=0，0＜b＜1的条件下，S的最大值；
（Ⅱ）当|AB|=2，S=1时，求直线AB的方程。
解：（Ⅰ）设点A的坐标为（x1，b），点B的坐标为（x2，b），
由
，解得
，
所以
，
当且仅当
时，S取得最大值1。
（Ⅱ）由
得
，
， ①
，②
设O到AB的距离为d，则
，
又因为
，
所以
，
代入②式并整理，得
，解得
，
代入①式检验，△＞0，
故直线AB的方程是
。
练习册系列答案
相关题目
如图，直线y=kx+b与椭圆
如图，直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分，求k的值．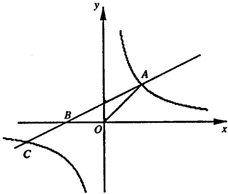
如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线y=（m+5）x2m+1交于点A、C，其中点A在第一象限，点C在第三象限．
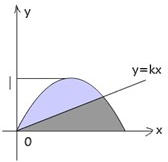如图，直线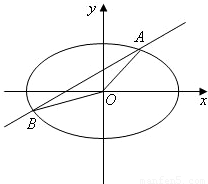
如图，直线y=kx+b与椭圆
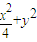=1交于A，B两点，记△AOB的面积为S．