题目内容
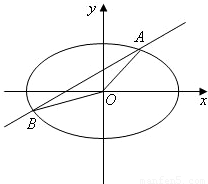 如图,直线y=kx+b与椭圆
如图,直线y=kx+b与椭圆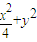 =1交于A,B两点,记△AOB的面积为S.
=1交于A,B两点,记△AOB的面积为S.(I)求在k=0,0<b<1的条件下,S的最大值;
(Ⅱ)当|AB|=2,S=1时,求直线AB的方程.
【答案】分析:(Ⅰ)设出点A,B的坐标利用椭圆的方程求得A,B的横坐标,进而利用弦长公式和b,求得三角形面积表达式,利用基本不等式求得其最大值.
(Ⅱ)把直线与椭圆方程联立,进而利用弦长公式求得AB的长度的表达式,利用O到直线AB的距离建立方程求得b和k的关系式,求得k.则直线的方程可得.
解答:解:(Ⅰ)设点A的坐标为(x1,b),点B的坐标为(x2,b),
由 ,解得
,解得 ,
,
所以 =
= ≤b2+1-b2=1.
≤b2+1-b2=1.
当且仅当 时,S取到最大值1.
时,S取到最大值1.
(Ⅱ)解:由
得 ,①
,①
△=4k2-b2+1,
 =
= .②
.②
设O到AB的距离为d,则 ,
,
又因为 ,
,
所以b2=k2+1,代入②式并整理,得 ,
,
解得 ,
, ,代入①式检验,△>0,
,代入①式检验,△>0,
故直线AB的方程是 或
或 或
或 ,或
,或 .
.
点评:本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.
(Ⅱ)把直线与椭圆方程联立,进而利用弦长公式求得AB的长度的表达式,利用O到直线AB的距离建立方程求得b和k的关系式,求得k.则直线的方程可得.
解答:解:(Ⅰ)设点A的坐标为(x1,b),点B的坐标为(x2,b),
由
 ,解得
,解得 ,
,所以
 =
= ≤b2+1-b2=1.
≤b2+1-b2=1.当且仅当
 时,S取到最大值1.
时,S取到最大值1.(Ⅱ)解:由

得
 ,①
,①△=4k2-b2+1,
 =
= .②
.②设O到AB的距离为d,则
 ,
,又因为
 ,
,所以b2=k2+1,代入②式并整理,得
 ,
,解得
 ,
, ,代入①式检验,△>0,
,代入①式检验,△>0,故直线AB的方程是
 或
或 或
或 ,或
,或 .
.点评:本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
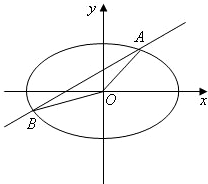 如图,直线y=kx+b与椭圆
如图,直线y=kx+b与椭圆 如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.
如图,直线y=kx分抛物线y=x-x2与x轴所围图形为面积相等的两部分,求k的值.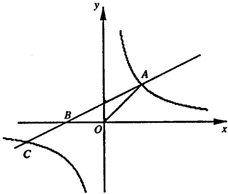 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.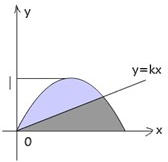 如图,直线
如图,直线