题目内容
已知定义域为[-2,2]的函数f(x)=
是奇函数.
(Ⅰ)求实数a,b的值;
(Ⅱ)解关于m的不等式f(m)+f(m-1)>f(0).
| -2x+b | 2x+1+a |
(Ⅰ)求实数a,b的值;
(Ⅱ)解关于m的不等式f(m)+f(m-1)>f(0).
分析:(Ⅰ)由奇函数可得,f(-x)+f(x)=0,据此可得关于a,b的方程组,解出即得a,b,注意取舍.
(Ⅱ)对f(x)进行变形后可判断其单调性,根据单调性及奇偶性可去掉不等式中的符号“f”,化为具体不等式,注意考虑定义域.
(Ⅱ)对f(x)进行变形后可判断其单调性,根据单调性及奇偶性可去掉不等式中的符号“f”,化为具体不等式,注意考虑定义域.
解答:解:(Ⅰ)由f(x)+f(-x)=0得:(2b-a)•(2x)2+(2ab-4)•2x+(2b-a)=0,
所以
,
解得:
或
,
又f(0)=0,即
=0,得b=1,且a≠-2,
因此
.
(Ⅱ)∵f(x)=
=
(-1+
),
∴函数f(x)在[-2,2]上单调递减,
由f(m)+f(m-1)>f(0)得:f(m)>f(1-m),
所以
,解得:-1≤m<
,
所以原不等式的解集为[-1,
).
所以
|
解得:
|
|
又f(0)=0,即
| -1+b |
| 2+a |
因此
|
(Ⅱ)∵f(x)=
| -2x+1 |
| 2x+1+2 |
| 1 |
| 2 |
| 2 |
| 2x+1 |
∴函数f(x)在[-2,2]上单调递减,
由f(m)+f(m-1)>f(0)得:f(m)>f(1-m),
所以
|
| 1 |
| 2 |
所以原不等式的解集为[-1,
| 1 |
| 2 |
点评:本题考查函数的奇偶性、单调性的综合及其应用,考查不等式的解法,属中档题.

练习册系列答案
相关题目
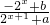 是奇函数.
是奇函数. ,若函数y=f(x)-m(x+1)有三个不同的零点,则实数m的取值范围为( )
,若函数y=f(x)-m(x+1)有三个不同的零点,则实数m的取值范围为( ) )
) ]
] ,
, ]
] )∪(
)∪( ,+∞)
,+∞)