题目内容
如图,在长方形ABCD中,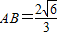 ,
,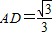 ,O为AB的中点,若P是线段DO上动点,则
,O为AB的中点,若P是线段DO上动点,则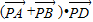 的最小值是 .
的最小值是 .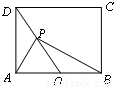
【答案】分析:由两个向量的加减法的法则,以及其几何意义可得,要求的式子即-2|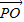 |•|
|•|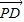 |.|
|.|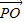 |+|
|+|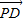 |=|
|=|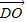 |=1,再利用基本不等式求得|
|=1,再利用基本不等式求得|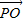 |•|
|•|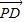 |≤
|≤ ,
,
从而求得-2|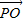 |•|
|•|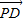 |的最小值.
|的最小值.
解答:解:由题意可得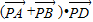 =2
=2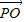 •
•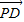 =-2|
=-2|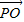 |•|
|•|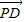 |.
|.
由于|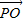 |+|
|+|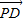 |=|
|=|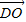 |=
|=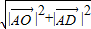 =
=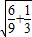 =1,且|
=1,且|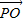 |+|
|+|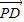 |≥2
|≥2 ,当且仅当|
,当且仅当|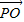 |=|
|=|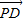 |时取等号.
|时取等号.
∴|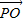 |•|
|•|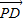 |≤
|≤ ,∴-2|
,∴-2|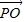 |•|
|•|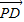 |≥-
|≥- ,∴
,∴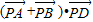 的最小值是-
的最小值是- ,
,
故答案为- .
.
点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,基本不等式的应用,属于中档题.
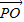 |•|
|•|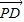 |.|
|.|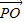 |+|
|+|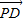 |=|
|=|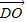 |=1,再利用基本不等式求得|
|=1,再利用基本不等式求得|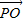 |•|
|•|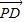 |≤
|≤ ,
,从而求得-2|
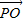 |•|
|•|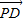 |的最小值.
|的最小值.解答:解:由题意可得
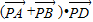 =2
=2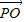 •
•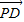 =-2|
=-2|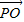 |•|
|•|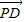 |.
|.由于|
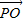 |+|
|+|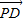 |=|
|=|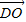 |=
|=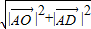 =
=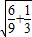 =1,且|
=1,且|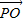 |+|
|+|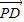 |≥2
|≥2 ,当且仅当|
,当且仅当|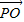 |=|
|=|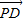 |时取等号.
|时取等号.∴|
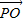 |•|
|•|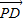 |≤
|≤ ,∴-2|
,∴-2|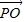 |•|
|•|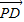 |≥-
|≥- ,∴
,∴ 的最小值是-
的最小值是- ,
,故答案为-
 .
.点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,基本不等式的应用,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
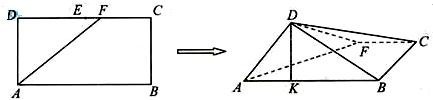
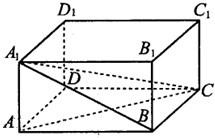 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
若一个n面体有m个面时直角三角形,则称这个n面体的直度为 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=