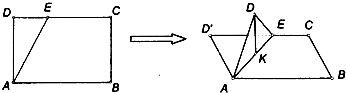
题目内容
 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=| 3 |
分析:由图形的翻折过程知,若连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,易知此圆半径是
,求得此弧所对的圆心角的弧度数,利用弧长公式求出轨迹长度.
| 1 |
| 2 |
解答: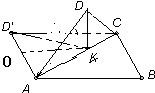 解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,易知此圆半径是
解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,易知此圆半径是
,
如图当E与C重合时,AK=
=
,取O为AD′的中点,则△OAK是正三角形.
故∠K0A=
∴∠K0D'=
其所对的弧长为
×
=
故答案为:
.
 解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,易知此圆半径是
解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,易知此圆半径是| 1 |
| 2 |
如图当E与C重合时,AK=
| 1×1 | ||
|
| 1 |
| 2 |
故∠K0A=
| π |
| 3 |
∴∠K0D'=
| 2π |
| 3 |
其所对的弧长为
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查多面体与旋转体表面上的最短距离问题,解题的关键是由题意得出点K的轨迹是圆上的一段弧,翻折问题中要注意位置关系与长度等数量的变与不变.本题比较抽象,考查了空间想像能力及根据所给的条件及图形位置关系进行推理论证的能力.

练习册系列答案
相关题目
 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
若一个n面体有m个面时直角三角形,则称这个n面体的直度为