题目内容
在数列{an}中，Sn=a1+a2+…+an,a1=1,an+1=
Sn(n≥1),则an= 。
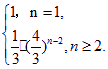
解析:
∵an+1=
Sn,∴an=Sn-1(n≥2).
相减得,an+1-an=an,∴
(n≥2)，
∵a2=S1=×1=,∴当n≥2时，an=·（
）n-2.
练习册系列答案
相关题目
解析:
题目内容
在数列{an}中，Sn=a1+a2+…+an,a1=1,an+1=Sn(n≥1),则an= 。
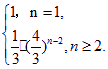
∵an+1=Sn,∴an=Sn-1(n≥2).
相减得,an+1-an=an,∴(n≥2)，
∵a2=S1=×1=,∴当n≥2时，an=·（）n-2.
，S3＝12＋
．
，
，…，
，…成等比数列，其中n1＝1，n2＝3，求nk（用k表示）；