题目内容
方程
的解集为 ．
【答案】分析：由已知中方程
，利用同角三角函数的关系式，我们可以将其转化为
，根据
，结合正切函数的周期性，即可得到答案．
解答：解：若程
即
∵
∴
∴
故方程
的解集为：
故答案为：
点评：本题考查的知识点是同角三角函数间的基本关系，正切函数的周期性，其中在解答时要注意正切函数的最小正周期为π，而不是2π．
，利用同角三角函数的关系式，我们可以将其转化为，根据，结合正切函数的周期性，即可得到答案．解答：解：若程
即
∵
∴
∴
故方程
的解集为：故答案为：
点评：本题考查的知识点是同角三角函数间的基本关系，正切函数的周期性，其中在解答时要注意正切函数的最小正周期为π，而不是2π．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若在直线l上存在不同的三个点A，B，C，使得关于实数x的方程x2
+x
+
=
有解（点O不在l上），则此方程的解集为（ ）
| OA |
| OB |
| BC |
| 0 |
| A、{-1} | ||||||||
| B、{0} | ||||||||
C、{
| ||||||||
| D、{-1，0} |
|=
的解集为( ) 
B.(-3，-2
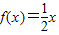，则方程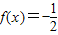
的解集为 ．