题目内容
 直四棱柱ABCD-A1B1C1D1中,AD=DC=
直四棱柱ABCD-A1B1C1D1中,AD=DC=| 1 | 2 |
(Ⅰ)求证:EF∥平面B1C1G;
(Ⅱ)当二面角G-C1B1-C为45?时,求CD与平面C1B1G所成的角.
分析:(I)取C1G的中点H,连EH,HB1,由直四棱柱的几何特征及已知中AB∥CD,DC=
AB,E,F,G分别为AD1,A1B1,AB中点,易得EHB1F为平行四边形,进而EF∥B1H,由线面平行的判定定理即可得到EF∥平面B1C1G.
(Ⅱ)过G作GK⊥BC,垂足为K,由等腰三角形“三线合一”的性质可得K为BC中点,结合直棱柱的结构特征,我们可得BB1⊥平面ABCD,作KT⊥B1C1,垂足为T,连GT,则∠GTK为二面角G-B1C1-C的平面角,结合二面角G-C1B1-C为45°,设GK=a,则TK=a,CD=
a,过C作CO⊥平面B1C1G,垂足为O,连DO,则DO为斜线DC在平面B1C1DG上的射影,∠CDO即为DC与平面B1C1G所成的角.解三角形CDO即可得到CD与平面C1B1G所成的角.
| 1 |
| 2 |
(Ⅱ)过G作GK⊥BC,垂足为K,由等腰三角形“三线合一”的性质可得K为BC中点,结合直棱柱的结构特征,我们可得BB1⊥平面ABCD,作KT⊥B1C1,垂足为T,连GT,则∠GTK为二面角G-B1C1-C的平面角,结合二面角G-C1B1-C为45°,设GK=a,则TK=a,CD=
| 2 |
解答:证明:(Ⅰ)取C1G的中点H,连EH,HB1.
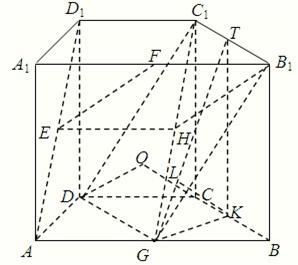 ∵AB∥CD,DC=
∵AB∥CD,DC=
AB,∴AG
CD,
又由直棱柱得,D1C1
DC,
∴AG
C1D1,∴四边形AGC1D1为平行四边形.
∵AE=ED1,GH=HC1,∴EH
AG.
∵FB1
AG.∴EH
B1F.∴EHB1F为平行四边形,∴EF∥B1H.
∵EF
平面B1C1G,B1H?平面B1C1G,∴EF∥平面B1C1G.
(Ⅱ)由条件得DG
BC,又∵BC
B1C1,∴DG
B1C1.∴平面B1C1G即为平面B1C1DG.
过G作GK⊥BC,垂足为K,∵GB=GC,∴K为BC中点,
∵ABCD-A1B1C1D1为直棱柱,∴BB1⊥平面ABCD.∴BB1⊥GK.
∴GK⊥平面BB1C1C,作KT⊥B1C1,
垂足为T,连GT,则GT⊥B1C1.
∴∠GTK为二面角G-B1C1-C的平面角,∴∠GTK=45°.
设GK=a,则TK=a,CD=
a,过C作CO⊥平面B1C1G,
垂足为O,连DO,则DO为斜线DC在平面B1C1DG上的射影,
∴∠CDO即为DC与平面B1C1G所成的角.
∵CB∥DG,DG?平面B1C1G,CB
平面B1C1DG,
∴BC∥平面B1C1DG.
∴点C到平面B1C1G的距离CO与点K到平面B1C1G的距离相等,
∵B1C1⊥GT,B1C1⊥TK,
∴B1C1⊥平面GKT,
∵B1C1?平面B1C1DG,
∴平面GKT⊥平面B1C1DG,过K作KL⊥GT,垂足为L,则KL⊥平面B1C1DG.
在△GKT中GK=KT=a,
∴KL=
a,即K到平面B1C1G的距离为
a,
∴CO=
a,在Rt△CDO中,CO=
a,CD=
a,
∴sin∠CDO=
,∠CDO=30°,
即直线CD与平面B1C1G所成的角为30°
 ∵AB∥CD,DC=
∵AB∥CD,DC=| 1 |
| 2 |
| ||
. |
又由直棱柱得,D1C1
| ||
. |
∴AG
| ||
. |
∵AE=ED1,GH=HC1,∴EH
| ||
. |
∵FB1
| ||
. |
| ||
. |
∵EF
| ||
. |
(Ⅱ)由条件得DG
| ||
. |
| ||
. |
| ||
. |
过G作GK⊥BC,垂足为K,∵GB=GC,∴K为BC中点,
∵ABCD-A1B1C1D1为直棱柱,∴BB1⊥平面ABCD.∴BB1⊥GK.
∴GK⊥平面BB1C1C,作KT⊥B1C1,
垂足为T,连GT,则GT⊥B1C1.
∴∠GTK为二面角G-B1C1-C的平面角,∴∠GTK=45°.
设GK=a,则TK=a,CD=
| 2 |
垂足为O,连DO,则DO为斜线DC在平面B1C1DG上的射影,
∴∠CDO即为DC与平面B1C1G所成的角.
∵CB∥DG,DG?平面B1C1G,CB
| ||
. |
∴BC∥平面B1C1DG.
∴点C到平面B1C1G的距离CO与点K到平面B1C1G的距离相等,
∵B1C1⊥GT,B1C1⊥TK,
∴B1C1⊥平面GKT,
∵B1C1?平面B1C1DG,
∴平面GKT⊥平面B1C1DG,过K作KL⊥GT,垂足为L,则KL⊥平面B1C1DG.
在△GKT中GK=KT=a,
∴KL=
| ||
| 2 |
| ||
| 2 |
∴CO=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴sin∠CDO=
| 1 |
| 2 |
即直线CD与平面B1C1G所成的角为30°
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,本题以常规的底面为直角梯形的直四棱柱为载体,考查学生线面平行的证明,用三垂线定理作二面角的平面角,找直线与平面交点,直线与平面所成的角等立体几何问题.突出基本方法与常规思路的应用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
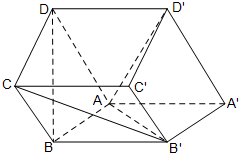 如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=
如图,在直四棱柱ABCD-A′B′C′D′中,底面ABCD为梯形,BC∥AD,AA′=AB=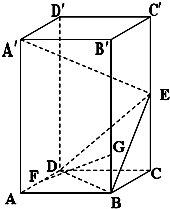 已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点.
已知直四棱柱ABCD-A′B′C′D′,四边形ABCD为正方形,AA′=2AB=2,E为棱CC′的中点.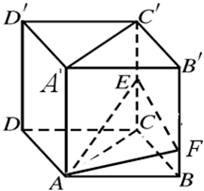 已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
已知直四棱柱ABCD-A′B′C′D′的底面是菱形,∠ABC=60°,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.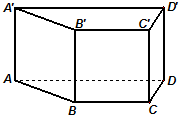 在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.
在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2. 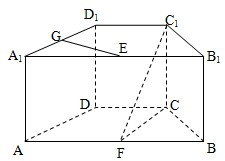 (2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
(2009•崇明县一模)如图,在直四棱柱ABCD-A'B'C'D'中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.