题目内容
(本小题满分12分)
已知等差数列{ }的前n项和为Sn,且
}的前n项和为Sn,且
 =
=
(1)求通项 ;
;
(2)求数列{ }的前n项和的最小值。
}的前n项和的最小值。
(1)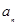 =4n-2(2)-225.
=4n-2(2)-225.
解析试题分析:(1)由 =10,
=10,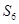 =72,得
=72,得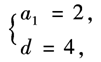
∴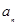 =4n-2,----------4
=4n-2,----------4
(2)则bn =
 -30=2n-31.
-30=2n-31.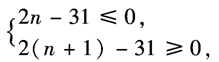
得 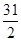 ≤n≤
≤n≤ -------------------10 .
-------------------10 .
∵n∈N*,∴n=15.
∴{ }前15项为负值,∴
}前15项为负值,∴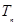 最小,---------------12
最小,---------------12
可知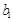 =-29,d=2,∴
=-29,d=2,∴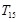 =-225.----------------------12
=-225.----------------------12
考点:本题考查了数列的通项及前n项和的性质
点评:等差数列的通项公式可化为 ,是关于
,是关于 的一次函数,当
的一次函数,当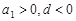 时为减函数且
时为减函数且 有最大值,取得最大值时的项数
有最大值,取得最大值时的项数 可由
可由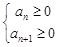 来确定;当
来确定;当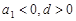 时为增函数且
时为增函数且 有最小值,取得最小值时的项数
有最小值,取得最小值时的项数 可由
可由 来确定.关键是要确定
来确定.关键是要确定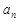 符号的转折点.
符号的转折点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 :
:
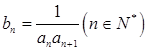 ,设
,设 ,求
,求 。
。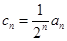 ,
, 为数列
为数列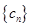 的前
的前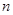 项和,求
项和,求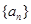 满足
满足 ,
,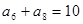
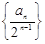 的前n项和.
的前n项和.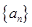 中,
中, 且
且 成等比数列,求数列
成等比数列,求数列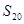 .
.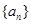 是等差数列,
是等差数列,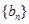 是公比为
是公比为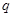 的等比数列,
的等比数列,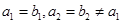 ,记
,记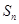 为数列
为数列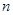 项和,
项和,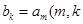 是大于
是大于 的正整数
的正整数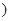 ,求证:
,求证: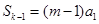 ;
;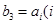 是某一正整数
是某一正整数 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数 构成等差数列
构成等差数列 ,
, 是
是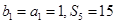

 ,求
,求 的值;
的值; ,求
,求 .
. 是公差不为零的等差数列,
是公差不为零的等差数列,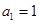 ,且
,且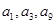 成等比数列.
成等比数列.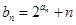 ,求数列
,求数列 的前
的前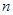 项和
项和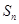
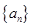 中,
中,  ,
, ,
, .
. 是等比数列;
是等比数列; 项和
项和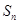 .
. 成立.
成立. =9a2a6.
=9a2a6. 的前n项和Tn;
的前n项和Tn; ≥ (7? 2n)Tn恒成立的实数k 的取值范围.
≥ (7? 2n)Tn恒成立的实数k 的取值范围.