题目内容
设点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为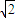 ,并记点P的轨迹为曲线C.
,并记点P的轨迹为曲线C.(I)求曲线C的方程;
(Ⅱ)设M(-2,0)的,过点M的直线l与曲线C相交于E,F两点,当线段EF的中点落在由四点C1(-1,0),C2(1,0),B1(0,-1),B2(0,1)构成的四边形内(不包括边界)时,求直线l斜率的取值范围.
【答案】分析:(I)利用点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为 ,建立方程,化简可得曲线C的方程;
,建立方程,化简可得曲线C的方程;
(Ⅱ)设出直线方程代入椭圆方程,利用韦达定理求出G的坐标,判断出G在正方形内,即可求得直线l斜率的取值范围.
解答: 解:(I)∵点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为
解:(I)∵点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为 ,
,
∴
∴
∴曲线C的方程为 ;
;
(Ⅱ)设直线l的方程为y=k(x+2),设E(x1,y1),F(x2,y2),线段EF的中点G(x,y),
直线方程代入椭圆方程可得(1+2k2)x2+8k2x+8k2-2=0
由△>0,可得
∵x1+x2= ,∴x=
,∴x= ,y=
,y=
∵x= ≤0,∴点G不可能在y轴的右边
≤0,∴点G不可能在y轴的右边
∵直线C1B2,C1B1的方程为y=x+1,y=-x-1
∴点G在正方形内的充要条件为 ,即
,即
∴ .
.
综上可知, .
.
点评:本题考查轨迹方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,综合性强.
 ,建立方程,化简可得曲线C的方程;
,建立方程,化简可得曲线C的方程;(Ⅱ)设出直线方程代入椭圆方程,利用韦达定理求出G的坐标,判断出G在正方形内,即可求得直线l斜率的取值范围.
解答:
 解:(I)∵点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为
解:(I)∵点P(x,y)到直线x=2的距离与它到定点(1,0)的距离之比为 ,
,∴

∴

∴曲线C的方程为
 ;
;(Ⅱ)设直线l的方程为y=k(x+2),设E(x1,y1),F(x2,y2),线段EF的中点G(x,y),
直线方程代入椭圆方程可得(1+2k2)x2+8k2x+8k2-2=0
由△>0,可得

∵x1+x2=
 ,∴x=
,∴x= ,y=
,y=
∵x=
 ≤0,∴点G不可能在y轴的右边
≤0,∴点G不可能在y轴的右边∵直线C1B2,C1B1的方程为y=x+1,y=-x-1
∴点G在正方形内的充要条件为
 ,即
,即
∴
 .
.综上可知,
 .
.点评:本题考查轨迹方程,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
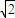 ,并记点M的轨迹为曲线C.
,并记点M的轨迹为曲线C.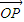 =
=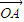 +
+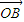 成立?若存在,求出直线l的方程;若不存在,说明理由.
成立?若存在,求出直线l的方程;若不存在,说明理由. ,并记点M的轨迹为曲线C.
,并记点M的轨迹为曲线C. =
= +
+ 成立?若存在,求出直线l的方程;若不存在,说明理由.
成立?若存在,求出直线l的方程;若不存在,说明理由.