题目内容
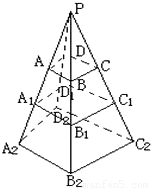 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
【答案】分析:本题考查的是棱台的侧面积和中截面的综合类问题.在解答时,首先要还台为锥充分结合侧面三角形的相似特征,根据面积比是相似比的特点,结合等比定理即可获得问题的解答.
解答:解:设A1B1C1D1是棱台ABCD-A2B2C2D2的中截面,延长各侧棱交于P点.
∵BC=a,B2C2=b∴B1C1= ∵BC∥B1C1∴
∵BC∥B1C1∴
∴
同理
∴ =
= =
= =
= =
=
同理:
由等比定理,得
故中截面把此棱台侧面分成的两部分面积之比为: .
.
点评:本题考查的是棱台的侧面积和中截面的综合类问题.在解答的过程当中充分体现了,还台为锥的思想、三角形相似的知识以及等比定理的知识.值得同学们体会反思.
解答:解:设A1B1C1D1是棱台ABCD-A2B2C2D2的中截面,延长各侧棱交于P点.
∵BC=a,B2C2=b∴B1C1=
 ∵BC∥B1C1∴
∵BC∥B1C1∴
∴

同理

∴
 =
= =
= =
= =
=
同理:

由等比定理,得

故中截面把此棱台侧面分成的两部分面积之比为:
 .
.点评:本题考查的是棱台的侧面积和中截面的综合类问题.在解答的过程当中充分体现了,还台为锥的思想、三角形相似的知识以及等比定理的知识.值得同学们体会反思.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
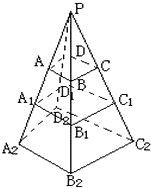 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
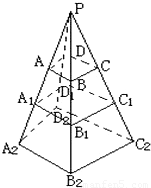 已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.
已知四棱台上,下底面对应边分别是a,b,试求其中截面把此棱台侧面分成的两部分面积之比.