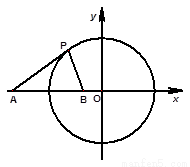
题目内容
已知圆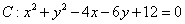 ,
点
,
点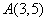 ,
,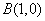 ,求;
,求;
(1)过点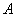 的圆C的切线方程;
的圆C的切线方程;
(2)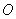 点是坐标原点,连结
点是坐标原点,连结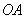 ,
,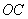 ,求
,求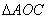 的面积
的面积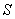 .
.
(3)设动圆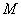 过点
过点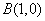 ,且圆心
,且圆心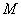 在抛物线
在抛物线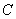 :
: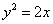 上,
上,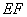 是圆
是圆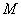 在
在 轴上截得的弦,当
轴上截得的弦,当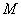 运动时弦长
运动时弦长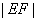 是否为定值?请说明理由.
是否为定值?请说明理由.
【答案】
解:(1)⊙
当切线的斜率不存在时,对直线 到直线
到直线
的距离为1,满足条件
当 存在时,设直线
存在时,设直线 ,即
,即 ,
,
得
∴得切线方程 或
或
(2)
直线 的方程为:
的方程为:
圆心C到直线 的距离
的距离


(3)设圆心 ,因为圆
,因为圆 过
过
故设圆的方程
令 得:
得:
设圆与 轴的两交点为
轴的两交点为 ,则
,则

∵ 在抛物线
在抛物线 上,
上,
 ,
,
所以,当 运动时,弦长
运动时,弦长 为定值2
为定值2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
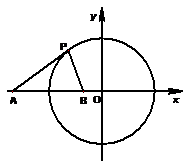 ⑴求与圆
⑴求与圆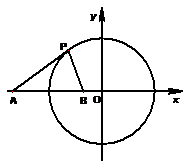
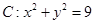 ,点
,点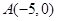 ,直线
,直线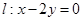 .
.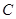 相切,且与直线
相切,且与直线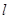 垂直的直线方程;
垂直的直线方程;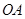 上(
上(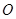 为坐标原点),存在定点
为坐标原点),存在定点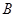 (不同于点
(不同于点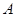 ),满足:对于圆
),满足:对于圆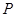 ,都有
,都有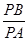 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点