题目内容
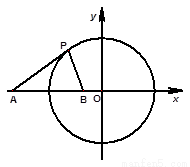
已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
⑴求与圆![]() 相切,且与直线
相切,且与直线![]() 垂直的直线方程;ks5u
垂直的直线方程;ks5u
⑵在直线![]() 上(
上(![]() 为坐标原点),存在定点
为坐标原点),存在定点![]() (不同于点
(不同于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标.
的坐标.
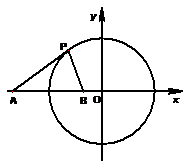
(1)![]()
(2)存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() 。
。
解析:
⑴设所求直线方程为![]() ,即
,即![]() ,
,
![]() 直线与圆相切,∴
直线与圆相切,∴![]() ,得
,得![]() ,
,
∴所求直线方程为![]()
⑵方法1:假设存在这样的点![]() ,
,
当![]() 为圆
为圆![]() 与
与![]() 轴左交点
轴左交点![]() 时,
时,![]() ;
;
当![]() 为圆
为圆![]() 与
与![]() 轴右交点
轴右交点![]() 时,
时,![]() ,
,
依题意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() 。
。
下面证明 点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数。
为一常数。
设![]() ,则
,则![]() ,
,
∴ ,
,
从而![]() 为常数。
为常数。
方法2:假设存在这样的点![]() ,使得
,使得![]() 为常数
为常数![]() ,则
,则![]() ,
,
∴![]() ,将
,将![]() 代入得,
代入得,
![]() ,即
,即
![]() 对
对![]() 恒成立,
恒成立,
∴ ,解得
,解得 或
或 (舍去),
(舍去),
所以存在点![]() 对于圆
对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为常数
为常数![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ⑴求与圆
⑴求与圆 ,
, 过点
过点 的直线,则( )
的直线,则( ) 相交 B.
相交 B. ,
, 过点
过点 的直线,则
的直线,则 的位置关系是___________(填“相交”、“相切”、“相离”或“三种位置关系均有可能”).
的位置关系是___________(填“相交”、“相切”、“相离”或“三种位置关系均有可能”). 过点
过点 的直线
的直线 将圆
将圆 分成弧长之比为
分成弧长之比为 的两段圆弧,则直线
的两段圆弧,则直线 ,点
,点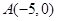 ,直线
,直线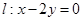 .
.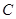 相切,且与直线
相切,且与直线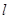 垂直的直线方程;
垂直的直线方程;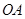 上(
上(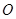 为坐标原点),存在定点
为坐标原点),存在定点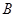 (不同于点
(不同于点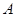 ),满足:对于圆
),满足:对于圆 ,都有
,都有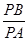 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点