题目内容
某单位有车牌尾号分别为0、5、6的汽车各一辆,分别记为A、B、C,已知在非限行日,根据工作需要每辆车可能出车或不出车,A、B、C三辆车每天出车的概率依次为
、
、
,且A、B、C三车出车相互独立,在限行日,不能出车,该地区汽车限行规定如下:
(Ⅰ)求该单位在星期四恰好出车两台的概率;
(Ⅱ)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
| 限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(Ⅱ)设X表示该单位在星期一与星期二两天的出车台数之和,求X的分布列及其数学期望E(X).
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)设A车在星期i出车的事件为Ai,B车在星期i出车的事件为Bi,C车在星期i出车的事件为Ci,
设该单位在星期四恰好出车两台为事件D,因为A,B,C两车是否出车相互独立,利用相互独立事件的概率公式求出该单位在星期四恰好出车两台的概率;
(Ⅱ)X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出
设该单位在星期四恰好出车两台为事件D,因为A,B,C两车是否出车相互独立,利用相互独立事件的概率公式求出该单位在星期四恰好出车两台的概率;
(Ⅱ)X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出
解答:
解:(Ⅰ)设A车在星期i出车的事件为Ai,B车在星期i出车的事件为Bi,C车在星期i出车的事件为Ci,
设该单位在星期四恰好出车两台为事件D
所以P(D)=P(A4B4
)+P(A4
C4)+P(
B4C4)=
×
×
+
×
×
+
×
×
=
(Ⅱ)X的可能取值是0,1,2,3
P(X=0)=P(
)P(
)=
×
×
=
P(X=1)=P(
)P(
)+P(
)P(A2
)+P(C1)P(
B2)
=
×
×
+
×
×
+
×
×
=
P(X=2)=P(
)P(A2B2)+P(C1)P(A2
)+P(C1)P(
B2)P(
B2)
=
×
×
+
×
×
+
×
×
=
=
P(X=3)=P(C1)P(A2B2)=
×
×
=
=
所以X的分布列
∴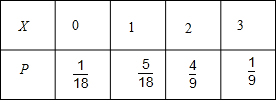
∴E(X)=0×
+1×
+2×
+3×
=
设该单位在星期四恰好出车两台为事件D
所以P(D)=P(A4B4
. |
| C4 |
. |
| B4 |
. |
| A4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 9 |
(Ⅱ)X的可能取值是0,1,2,3
P(X=0)=P(
. |
| C1 |
. |
| A2 |
. |
| B2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 18 |
P(X=1)=P(
. |
| C1 |
. |
| A2 |
. |
| B2 |
. |
| C1 |
. |
| B2 |
. |
| A2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 5 |
| 18 |
P(X=2)=P(
. |
| C1 |
. |
| B2 |
. |
| A2 |
. |
| A2 |
=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 18 |
| 4 |
| 9 |
P(X=3)=P(C1)P(A2B2)=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 18 |
| 2 |
| 9 |
所以X的分布列
∴

∴E(X)=0×
| 1 |
| 18 |
| 5 |
| 18 |
| 8 |
| 18 |
| 4 |
| 18 |
| 11 |
| 6 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
