题目内容
设二次函数f（x）满足f（x+2）=f（2-x），且f（x）=0的两实数根分别为3和1，图象过点（0，3）．
（1）求f（x）的解析式；
（2）求函数f（x）在区间[-1，3]上的最大值．
（1）求f（x）的解析式；
（2）求函数f（x）在区间[-1，3]上的最大值．
分析：（1）设y=ax2+bx+c（a≠0），由题意得，c=3，-
=2，
=3，由此能求出f（x）．
（2）由f（x）的对称轴x=2，能求出f（x）在区间[-1，3]上的最大值．
| b |
| 2a |
| c |
| a |
（2）由f（x）的对称轴x=2，能求出f（x）在区间[-1，3]上的最大值．
解答：解：（1）设y=ax2+bx+c（a≠0），
由题意得，c=3，-
=2，
=3，
∴a=1，b=-4，
∴f（x）=x2-4x+3
（2）∵f（x）=x2-4x+3，
∴f（x）=x2-4x+3的对称轴x=2，
∴f（x）=x2-4x+3在区间[-1，3]上的最大值为f（-1）=8．
由题意得，c=3，-
| b |
| 2a |
| c |
| a |
∴a=1，b=-4，
∴f（x）=x2-4x+3
（2）∵f（x）=x2-4x+3，
∴f（x）=x2-4x+3的对称轴x=2，
∴f（x）=x2-4x+3在区间[-1，3]上的最大值为f（-1）=8．
点评：本题考查函数的解析式的求法，考查函数的最大值的求法．解题时要认真审题，仔细解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(a＞0)，方程f(x)－x=0的两根
、
满足
，当
时，证明：
．
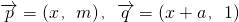，二次函数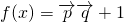
，关于x的不等式f（x）＞（2m-1）x+1-m2的解集为（-∞，m）∪（m+1，+∞），其中m为非零常数，设
．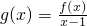