题目内容
9.设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时f(x)=($\frac{1}{2}$)x-1,若关于x的方程f(x)-loga(x+2)=0(a>1)在区间[-2,6]内恰有三个不同的实根,则实数a的取值范围是($\root{3}{4}$,2).分析 由已知中可以得到函数f(x)的图象关于直线x=2对称,结合函数是偶函数,及x∈[-2,0]时的解析式,可画出函数的图象,将方程f(x)-loga(x+2)=0恰有3个不同的实数解,转化为函数f(x)的与函数y=loga(x+2)的图象恰有3个不同的交点,数形结合即可得到实数a的取值范围.
解答 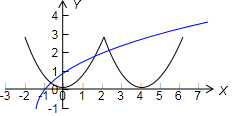 解:∵对于任意的x∈R,都有f(2-x)=f(x+2),
解:∵对于任意的x∈R,都有f(2-x)=f(x+2),
∴函数f(x)的图象关于直线x=2对称,
又∵当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,且函数f(x)是定义在R上的偶函数,
若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=loga(x+2)在区间(-2,6)上有三个不同的交点,如下图所示:
又f(-2)=f(2)=3,则有loga(2+2)<3,且loga(6+2)>3,
解得:$\root{3}{4}$<a<2,
故答案为:($\root{3}{4}$,2).
点评 本题考查的知识点是根的存在性及根的个数判断,指数函数与对数函数的图象与性质,其中根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题,是解答本题的关键,体现了转化和数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
17.点M为直线5x+12y=0上任一点,F1(-13,0),F2(13,0),则下列结论正确的是( )
| A. | ||MF1|-|MF2||>24 | B. | ||MF1|-|MF2||=24 | C. | ||MF1|-|MF2||<24 | D. | 以上都有可能 |
1.若f(x)=x2+2cosx,当α、β∈(-$\frac{π}{2}$,$\frac{π}{2}$)时,有f(α)>f(β),则( )
| A. | α>β | B. | α<β | C. | α2>β2 | D. | α+β>0 |
19.(1+2x)3(2-x)4的展开式中x的系数是( )
| A. | 96 | B. | 64 | C. | 32 | D. | 16 |
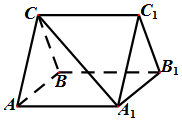 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.