题目内容
在一段时间内，某种商品的价格x（元／件）和需求量y（件）之间的一组数据为：
求出y对x的回归直线方程，并说明拟合效果的好坏。
解：
=14×12+16×10+18×7+20×5+22×3=620，
∴
=
=-1.15，
，
∴回归直线方程为
，
列出残差表为
∴
，
∴
，
∴R2≈0.994，
因而拟合效果较好。
=14×12+16×10+18×7+20×5+22×3=620，∴
==-1.15，，∴回归直线方程为
，列出残差表为
∴
，∴
，∴R2≈0.994，
因而拟合效果较好。
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
在一段时间内，某种商品的价格
（元）和需求量
（件）之间的一组数据如下表所示：
| 价格 | 14 | 16 | 18 | 20 | 22 |
| 需求量 | 12 | 10 | 7 | 5 | 3 |
求出对的回归直线方程，并说明拟合效果的好坏.
在一段时间内，某种商品的价格x（万元）和需求量Y（t）之间的一组数据为：
（1）在右面的坐标系中画出散点图；
（2）求出Y对x的回归直线方程
=
；（其中：
=
，
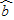参考数据1.42+1.62+1.82+22+2.22=16.6）
（3）回答下列问题：
（i）若价格定为1.9万元，预测需求量大约是多少？（精确到0.01t）
（ii）当价格定为多少时，商品将出现滞销？（精确到0.01万元）
（iii）当价格定为多少时，获得的收益最大？
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | 5 | 3 |
（2）求出Y对x的回归直线方程
=；（其中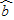：=，参考数据1.42+1.62+1.82+22+2.22=16.6）
| 序号 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 求和 |
（i）若价格定为1.9万元，预测需求量大约是多少？（精确到0.01t）
（ii）当价格定为多少时，商品将出现滞销？（精确到0.01万元）
（iii）当价格定为多少时，获得的收益最大？
在一段时间内，某种商品的价格x（万元）和需求量Y（t）之间的一组数据为：
（1）在右面的坐标系中画出散点图；
（2）求出Y对x的回归直线方程
=
；（其中：
=
，
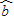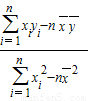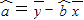
参考数据1.42+1.62+1.82+22+2.22=16.6）
（3）回答下列问题：
（i）若价格定为1.9万元，预测需求量大约是多少？（精确到0.01t）
（ii）当价格定为多少时，商品将出现滞销？（精确到0.01万元）
（iii）当价格定为多少时，获得的收益最大？
| 价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
| 需求量Y | 12 | 10 | 7 | 5 | 3 |
（2）求出Y对x的回归直线方程
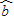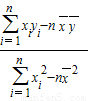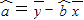
=；（其中：=，参考数据1.42+1.62+1.82+22+2.22=16.6）
| 序号 | ||||
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 求和 |
（i）若价格定为1.9万元，预测需求量大约是多少？（精确到0.01t）
（ii）当价格定为多少时，商品将出现滞销？（精确到0.01万元）
（iii）当价格定为多少时，获得的收益最大？