题目内容
10.已知集合A={2a,a2-a},则a的取值范围是{a|a≠0且a≠3}.分析 根据集合元素的互异性,进行求解范围
解答 解:根据集合元素的互异性可知,a2-a≠2a,即a≠0且a≠3.
所以a的取值范围{a|a≠0且a≠3}.
故答案为:{a|a≠0且a≠3}.
点评 本题主要考查元素的互异性的应用,比较基础.

练习册系列答案
相关题目
5.对?a,b∈R,记min{a,b}=$\left\{\begin{array}{l}{a,(a<b)}\\{b(a≥b)}\end{array}\right.$,则函数f(x)=min{|x+1|,|x-1|}(x∈R)的单调增区间为( )
| A. | [0,+∞) | B. | (-∞,0] | C. | (-∞,-1]和[0,1] | D. | [-1,0]和[1,+∞) |
2.若关于x的不等式x2+ax-c<0的解集为{x|-2<x<1},且函数y=ax3+mx2+x+$\frac{c}{2}$在区间($\frac{1}{2}$,1)上不是单调函数,则实数m的取值范围是( )
| A. | (-2,-$\sqrt{3}$) | B. | (-∞,-2)∪($\sqrt{3}$,+∞) | C. | [-3,-$\sqrt{3}$] | D. | (-∞,-2)∪(-$\sqrt{3}$,+∞) |
20.若复数x2-1+(x+1)i是纯虚数(i是虚数单位,x∈R),则x=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
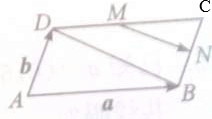 如图,?ABCD中,M、N分别是边DC、BC的中点.
如图,?ABCD中,M、N分别是边DC、BC的中点.