题目内容
在复数范围内解方程|z|2+(z+. |
| z |
| 3-i |
| 2+i |
分析:首先对等式的右边进行复数的除法运算,得到最简形式,设出要求的复数的结果,把设出的结果代入等式,根据复数相等的充要条件写出关于x的方程,解方程即可.
解答:解:原方程化简为|z|2+(z+
)i=1-i,
设z=x+yi(x、y∈R),
代入上述方程得x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,
解得x=-
且y=±
,
∴原方程的解是z=-
±
i.
. |
| z |
设z=x+yi(x、y∈R),
代入上述方程得x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,
解得x=-
| 1 |
| 2 |
| ||
| 2 |
∴原方程的解是z=-
| 1 |
| 2 |
| ||
| 2 |
点评:本题主要考查复数的除法和乘方运算,考查复数相等的充要条件,是一个基础题,解题时没有规律和技巧可寻,只要认真完成,则一定会得分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
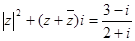 .(i为虚数单位)
.(i为虚数单位)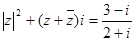 (i为虚数单位)
(i为虚数单位) 是实数,且-1<ω<2
是实数,且-1<ω<2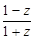 ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)