题目内容
(1)求值:
-(
)0+0.25
×(
)-4;
(2)求值:(lg2)2+lg5•lg20+lg100;
(3)已知5a=3,5b=4.求a、b,并用a,b表示log2512.
| 3 | (-4)3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
(2)求值:(lg2)2+lg5•lg20+lg100;
(3)已知5a=3,5b=4.求a、b,并用a,b表示log2512.
分析:(1)(2)根据对数运算法则和有理数指数幂的化简规则进行化简求值;
(3)根据对数运算法则已知5a=3,5b=4,两边取对数求出a,b,再根据对数法则表示出log2512.
(3)根据对数运算法则已知5a=3,5b=4,两边取对数求出a,b,再根据对数法则表示出log2512.
解答:解:(1)原式=-4-1+
×(
)4=-3; …(4分)
(2)原式=(lg2)2+(1-lg2)•(1+lg2)+2=(lg2)2+1-(lg2)2+2=3…(8分)
(3)∵5a=3,5b=4.
∴a=log53,b=log54…(10分)
∴log2512=
=
=
…(13分)
| 1 |
| 4 |
| 2 |
(2)原式=(lg2)2+(1-lg2)•(1+lg2)+2=(lg2)2+1-(lg2)2+2=3…(8分)
(3)∵5a=3,5b=4.
∴a=log53,b=log54…(10分)
∴log2512=
| log512 |
| log525 |
| log53+log53 |
| 2 |
| a+b |
| 2 |
点评:此题主要考查对数和指数运算法则和有理数指数幂的化简求值问题,是一道基础题;

练习册系列答案
相关题目
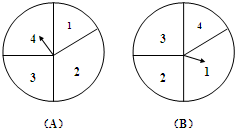 (2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.
(2010•珠海二模)如图是两个独立的转盘(A)、(B),在两个图中的四个扇形区域的圆心角分别为60°、120°、90°90°.用这两个转盘进行玩游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域数为x,转盘(B)指针所对的区域数为y,x、y∈{1,2,3,4},设x+y的值为ξ,每一次游戏得到奖励分为ξ.