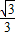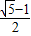Question

已知椭圆焦点在x轴，中心在原点，过左焦点F₁作垂直于x轴的弦AB，使得△ABF₂为正三角形，则椭圆的离心率为（　　）

• A．

  1

  2

• B．

  3

  3

• C．

  2

  3

• D．

  5 -1

  2

Answer 1

分析：由题意推出，|F₁F₂|是该正三角形的高，结合椭圆的定义求出a，然后求出椭圆的离心率．

解答：解：三角形△ABF₂是正三角形，|F₁F₂|是该正三角形的高，
设AF₁=m，由题意 AF₂=2m，
|AF₁|+|AF₂|=2a，
且|F₁F₂|=2c=

3

m 离心率e=

c

a

=

3 m

3m

=

3

3

故选B．

点评：本题是基础题，考查椭圆的定义的应用，充分利用三角形是正三角形是解题的关键，考查计算能力．