题目内容
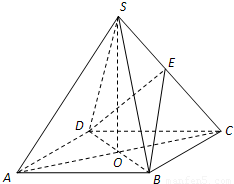
如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC;
(Ⅲ)(理科)当二面角E-BD-C的大小为45°时,试判断点E在SC上的位置,并说明理由.
【答案】分析:(I)做出辅助线,连接OE,由条件可得SA∥OE.根据因为SA?平面BDE,OE?平面BDE,得到SA∥平面BDE.
(II)建立坐标系,写出要用的点的坐标,写出要用的向量的坐标,设出平面的法向量,根据法向量与平面上的向量垂直,写出一个法向量,根据两个法向量垂直证明两个平面垂直.
(III)本题是一个一个二面角为条件,写出点的位置,做法同求两个平面的夹角一样,设出求出法向量,根据两个向量的夹角得到点要满足的条件,求出点的位置.
解答:解:(Ⅰ)证明:连接OE,由条件可得SA∥OE.
因为SA?平面BDE,OE?平面BDE,所以SA∥平面BDE.
(Ⅱ)证明:由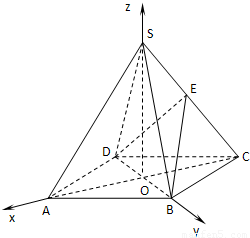 (Ⅰ)知SO⊥面ABCD,AC⊥BD.建立如图所示的空间直角坐标系.
(Ⅰ)知SO⊥面ABCD,AC⊥BD.建立如图所示的空间直角坐标系.
设四棱锥S-ABCD的底面边长为2,
则O(0,0,0),S(0,0,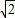 ),A(
),A(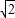 ,0,0),
,0,0),
B(0,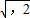 ,0),C(-
,0),C(-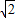 ,0,0),D(0,-
,0,0),D(0,-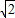 ,0).
,0).
所以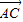 =(-2
=(-2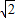 0,0),
0,0),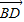 =(0,
=(0,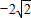 ,0).
,0).
设CE=a(0<a<2),由已知可求得∠ECO=45°.
所以E(-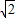 +
+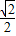 a,0,
a,0,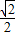 a),
a),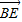 =(-
=(-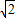 +
+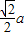 ,-
,-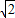 ,
,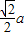 ).
).
设平面BDE法向量为n=(x,y,z),则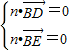 即
即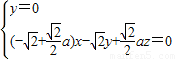
令z=1,得n=(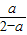 ,0,1).易知
,0,1).易知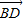 =(0,
=(0,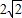 ,0)是平面SAC的法向量.
,0)是平面SAC的法向量.
因为n•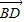 =(
=(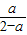 ,0,1)•(0,-
,0,1)•(0,-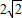 ,0)=0,所以n⊥
,0)=0,所以n⊥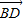 ,所以平面BDE⊥平面SAC.(8分)
,所以平面BDE⊥平面SAC.(8分)
(Ⅲ)设CE=a(0<a<2),由(Ⅱ)可知,平面BDE法向量为n=(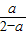 ,0,1).因为SO⊥底面ABCD,
,0,1).因为SO⊥底面ABCD,
所以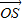 =(0,0,
=(0,0,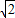 )是平面SAC的一个法向量.由已知二面角E-BD-C的大小为45°.
)是平面SAC的一个法向量.由已知二面角E-BD-C的大小为45°.
所以|cos(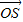 ,n)|=cos45°=
,n)|=cos45°=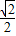 ,所以
,所以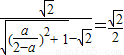 ,解得a=1.
,解得a=1.
所以点E是SC的中点.
点评:本题考查用空间向量解决线线角和面面角,本题解题的关键是建立坐标系,把立体几何的理论推导变化成数字的运算问题,这样可以降低题目的难度,同学们只要细心都可以做对.
(II)建立坐标系,写出要用的点的坐标,写出要用的向量的坐标,设出平面的法向量,根据法向量与平面上的向量垂直,写出一个法向量,根据两个法向量垂直证明两个平面垂直.
(III)本题是一个一个二面角为条件,写出点的位置,做法同求两个平面的夹角一样,设出求出法向量,根据两个向量的夹角得到点要满足的条件,求出点的位置.
解答:解:(Ⅰ)证明:连接OE,由条件可得SA∥OE.
因为SA?平面BDE,OE?平面BDE,所以SA∥平面BDE.
(Ⅱ)证明:由
 (Ⅰ)知SO⊥面ABCD,AC⊥BD.建立如图所示的空间直角坐标系.
(Ⅰ)知SO⊥面ABCD,AC⊥BD.建立如图所示的空间直角坐标系.设四棱锥S-ABCD的底面边长为2,
则O(0,0,0),S(0,0,
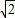 ),A(
),A(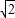 ,0,0),
,0,0),B(0,
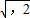 ,0),C(-
,0),C(-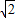 ,0,0),D(0,-
,0,0),D(0,-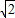 ,0).
,0).所以
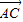 =(-2
=(-2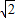 0,0),
0,0),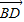 =(0,
=(0,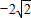 ,0).
,0).设CE=a(0<a<2),由已知可求得∠ECO=45°.
所以E(-
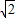 +
+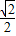 a,0,
a,0,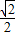 a),
a),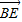 =(-
=(-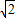 +
+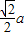 ,-
,-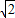 ,
,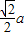 ).
).设平面BDE法向量为n=(x,y,z),则
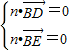 即
即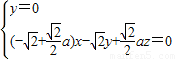
令z=1,得n=(
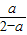 ,0,1).易知
,0,1).易知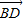 =(0,
=(0,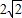 ,0)是平面SAC的法向量.
,0)是平面SAC的法向量.因为n•
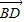 =(
=(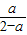 ,0,1)•(0,-
,0,1)•(0,-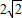 ,0)=0,所以n⊥
,0)=0,所以n⊥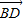 ,所以平面BDE⊥平面SAC.(8分)
,所以平面BDE⊥平面SAC.(8分)(Ⅲ)设CE=a(0<a<2),由(Ⅱ)可知,平面BDE法向量为n=(
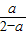 ,0,1).因为SO⊥底面ABCD,
,0,1).因为SO⊥底面ABCD,所以
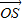 =(0,0,
=(0,0,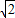 )是平面SAC的一个法向量.由已知二面角E-BD-C的大小为45°.
)是平面SAC的一个法向量.由已知二面角E-BD-C的大小为45°.所以|cos(
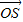 ,n)|=cos45°=
,n)|=cos45°=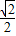 ,所以
,所以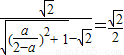 ,解得a=1.
,解得a=1.所以点E是SC的中点.
点评:本题考查用空间向量解决线线角和面面角,本题解题的关键是建立坐标系,把立体几何的理论推导变化成数字的运算问题,这样可以降低题目的难度,同学们只要细心都可以做对.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,