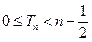题目内容
(本题满分12分)已知各项均为正数的数列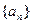 的前
的前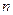 项和满足
项和满足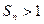 ,且
,且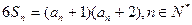 .(1)求
.(1)求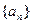 的通项公式;(2)设数列
的通项公式;(2)设数列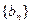 满足
满足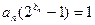 ,并记
,并记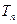 为
为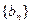 的前
的前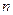 项和,比较
项和,比较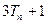 与
与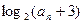 的大小.
的大小.
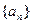 的前
的前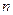 项和满足
项和满足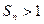 ,且
,且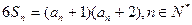 .(1)求
.(1)求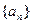 的通项公式;(2)设数列
的通项公式;(2)设数列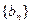 满足
满足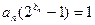 ,并记
,并记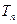 为
为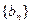 的前
的前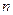 项和,比较
项和,比较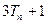 与
与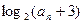 的大小.
的大小.(Ⅰ) 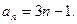 (Ⅱ)
(Ⅱ) 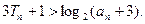
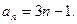 (Ⅱ)
(Ⅱ) 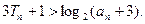
(Ⅰ)解:由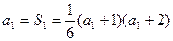 ,解得
,解得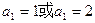 ,由假设
,由假设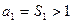 ,因此
,因此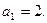 又由
又由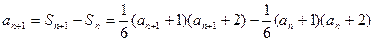 ,
,
得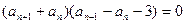 ,
,
即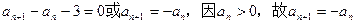 不成立,舍去。
不成立,舍去。
因此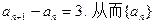 是公差为3,首项为2的等差数列,故{an}的通项为
是公差为3,首项为2的等差数列,故{an}的通项为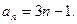
(Ⅱ)证法一:由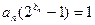 可解得
可解得 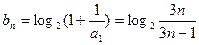
从而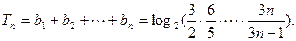
因此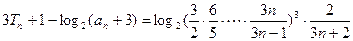
令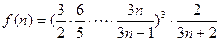 ,则
,则

因
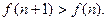
特别地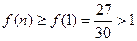 . 从而
. 从而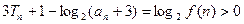 ,
,
即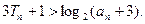
证法二:同证法一求得bn及Tn。由二项式定理知. 当c>0时,不等式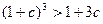 成立,
成立,
由此不等式有
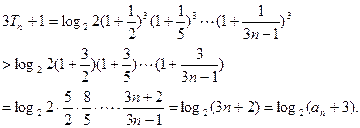
证法三:同证法一求得bn及Tn
令
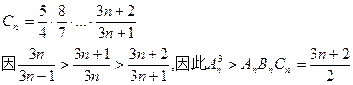
从而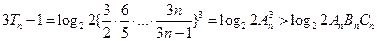
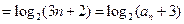
证法四:同证法一求得bn及Tn下面用数学归纳法证明: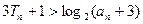
当n=1时,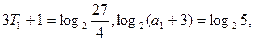
因此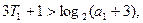 结论成立,
结论成立,
假设结论当n=k时成立,即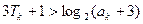
则当n=k+1时,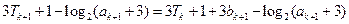
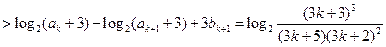
因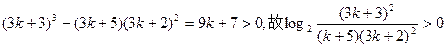
从而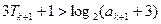 这就是说,当n=k+1时结论也成立
这就是说,当n=k+1时结论也成立
综上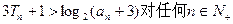 成立.
成立.
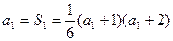 ,解得
,解得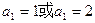 ,由假设
,由假设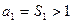 ,因此
,因此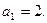 又由
又由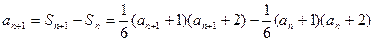 ,
,得
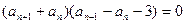 ,
,即
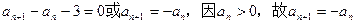 不成立,舍去。
不成立,舍去。因此
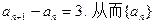 是公差为3,首项为2的等差数列,故{an}的通项为
是公差为3,首项为2的等差数列,故{an}的通项为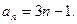
(Ⅱ)证法一:由
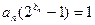 可解得
可解得 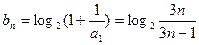
从而
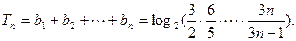
因此
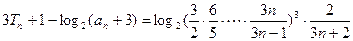
令
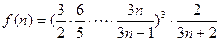 ,则
,则
因

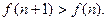
特别地
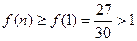 . 从而
. 从而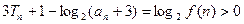 ,
,即
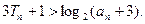
证法二:同证法一求得bn及Tn。由二项式定理知. 当c>0时,不等式
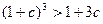 成立,
成立,由此不等式有
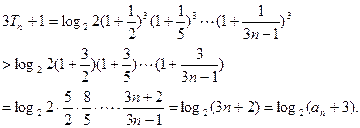
证法三:同证法一求得bn及Tn
令

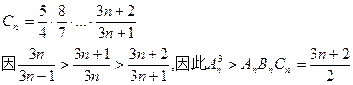
从而
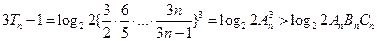
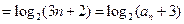
证法四:同证法一求得bn及Tn下面用数学归纳法证明:
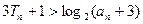
当n=1时,
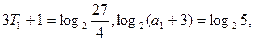
因此
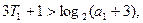 结论成立,
结论成立,假设结论当n=k时成立,即
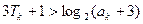
则当n=k+1时,
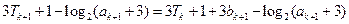
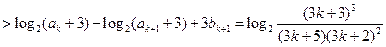
因
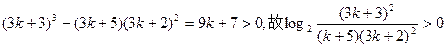
从而
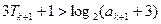 这就是说,当n=k+1时结论也成立
这就是说,当n=k+1时结论也成立综上
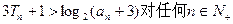 成立.
成立.
练习册系列答案
相关题目
 ,其中
,其中 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列; 是公差为
是公差为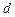 的等差数列;
的等差数列;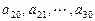 是公差为
是公差为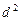 的等差数列(
的等差数列(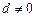 ).
).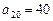 ,求
,求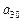 关于
关于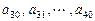 是公差为
是公差为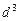 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?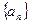 的前
的前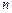 项和为
项和为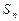 ,若
,若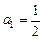 且
且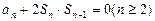 .
.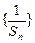 是等差数列,并求出
是等差数列,并求出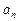 的表达式;
的表达式;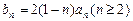 ,求证
,求证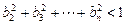 .
. 中,
中,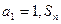 是数列
是数列 项和,对任意
项和,对任意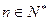 ,均有
,均有 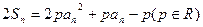 (1).求常数
(1).求常数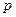 的值;(2)求数列
的值;(2)求数列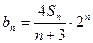 ,求数列
,求数列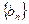 的前
的前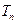 。
。 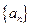 满足
满足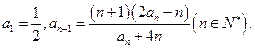
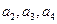 ;(Ⅱ)已知存在实数
;(Ⅱ)已知存在实数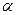 ,使
,使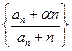 为公差为
为公差为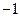 的等差数列,求
的等差数列,求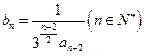 ,数列
,数列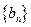 的前
的前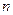 项和为
项和为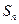 ,求证:
,求证: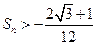 .
.
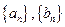 满足
满足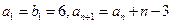 ,
,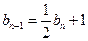
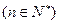 。
。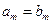 的正整数
的正整数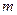 的集合M。
的集合M。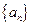 中,
中,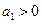 ,且
,且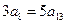 ,则
,则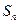 中最大的是 ()
中最大的是 ()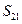
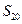
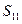
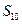
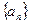 的首项
的首项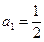 ,前n项和
,前n项和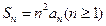
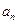 ;(2)记
;(2)记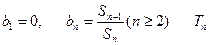 为数例
为数例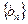 的前
的前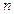 项和,求证
项和,求证