设P={x|x2-6x-16＜0}.Q={x|xA．{x|x＞-2}B．{x|-2＜x＜8}C．{x|3＜x＜8}D．{x|-2＜x＜3] 题目和参考答案——青夏教育精英家教网——

题目内容

19．设P={x|x²-6x-16＜0}，Q={x|x（x-1）＞6}，则P∩Q=（　　）

A．

{x|x＞-2}

B．

{x|-2＜x＜8}

C．

{x|3＜x＜8}

D．

{x|-2＜x＜3]

分析解不等式求出集合P，Q，结合集合的交集运算，可得答案．

解答解：∵P={x|x²-6x-16＜0}={x|-2＜x＜8}，
Q={x|x（x-1）＞6}={x|x＜-2，或x＞3}，
∴P∩Q={x|3＜x＜8}，
故选：C

点评本题考查的知识点是集合的交集，并集，补集运算，难度不大，属于基础题目．

练习册系列答案

专项卷和真题卷系列答案

文曲星中考总复习系列答案

问题引领系列答案

先锋题典系列答案

知识大集结系列答案

随堂口算系列答案

小学升学夺冠系列答案

培优好题系列答案

培优60课系列答案

解决问题专项训练系列答案

相关题目

9．已知双曲线$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}=1$的焦点为F₁，F₂，双曲线与椭圆$\frac{{x}^{2}}{29}+\frac{{y}^{2}}{4}=1$交于点P，则|PF₁|•|PF₂|的值为13．

10．方程2^x+x=0的解的个数是1．

7．（1）f（x）=|log_ax|，（0＜a＜1）减区间为（0，1]．
（2）直线y=2a与y=|a^x-1|，a＞0的图象有两个公共点，则a范围（0，$\frac{1}{2}$）．

14．已知2^x=3，y=log${\;}_{4}\frac{8}{3}$，利用换底公式，计算x+2y的值为3．

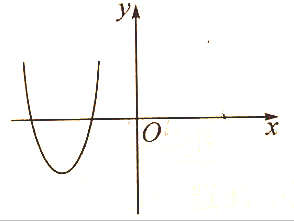已知函数f（x）是定义在R上的奇函数，其部分图象如图所示，则这个函数的零点至少有5个．

11．（1）化简下式：$\frac{\sqrt{{a}^{3}{b}^{2}•\root{3}{a{b}^{2}}}}{（{a}^{\frac{1}{4}}{b}^{\frac{1}{2}}）^{4}•\root{3}{\frac{b}{a}}}$（a＞0，b＞0）；
（2）已知x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$=$\sqrt{5}$，求下列各式的值：
①$\frac{{x}^{\frac{3}{2}}+{x}^{-\frac{3}{2}}+2}{{x}^{2}+{x}^{-2}}$+3；
②x²-x^-2．

8．已知a＞0，b＞0，则（2a^-3b${\;}^{-\frac{2}{3}}$）•（-3a^-1b）÷（4a^-4b${\;}^{-\frac{5}{3}}$）=（　　）

-$\frac{3}{2}$b²

$\frac{3}{2}$b²

-$\frac{3}{2}$b${\;}^{\frac{7}{3}}$

$\frac{3}{2}$b${\;}^{\frac{7}{3}}$

9．已知f（x）为R上的奇函数，当x＞0时，f（x）=-2x²+3x+1，求f（x）的解析式．