题目内容
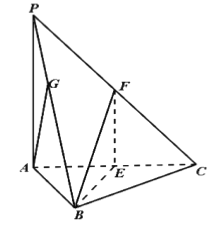
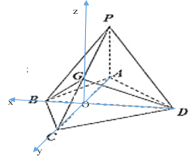
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 为线段
为线段![]() 的中点.
的中点.
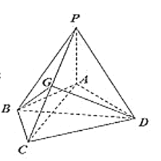
(1)证明:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据已知条件证明![]() ,结合
,结合![]() 平面
平面![]() .即可得证;
.即可得证;
(2)解法一(几何法):先找到![]() 在平面内的射影直线,则所求角可得,在直角三角形中求出此角,即可得结果;
在平面内的射影直线,则所求角可得,在直角三角形中求出此角,即可得结果;
解法二(空间向量法):建立空间直角坐标系,确定各点坐标,求出![]() 坐标和平面
坐标和平面![]() 的法向量坐标,结合线面角公式,即可得结果.
的法向量坐标,结合线面角公式,即可得结果.
(1)取![]() 中点
中点![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,∴
,∴![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 面
面![]() .
.
(2)法一:连结![]() ,由(1)
,由(1)![]() 平面
平面![]() 可得
可得![]() ,
,
![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
∴在![]() 中,
中,
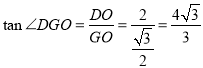 ,
,
∴![]() .
.
因此![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.
法二:以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 平行于
平行于![]() 的直线
的直线
为![]() ,
,![]() ,
,![]() 轴,建立如图所示空间直角坐标系,则因为
轴,建立如图所示空间直角坐标系,则因为
![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,因此
,因此![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
从而![]() 为平面
为平面![]() 一个法向量,
一个法向量,
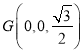 ,
,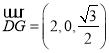 ,
,
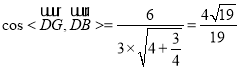 .
.
因此![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,其中女性有
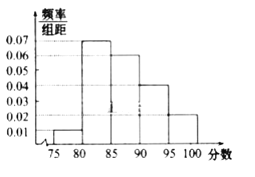
名观众进行调查,其中女性有![]() 名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
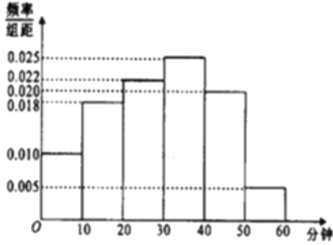
将日均收看该体育节目时间不低于![]() 分钟的观众称“体育述”,已知“体育迷”中
分钟的观众称“体育述”,已知“体育迷”中![]() 名女性.
名女性.
(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否认为“体育迷”与性別有关?
列联表,并据此资料你是否认为“体育迷”与性別有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
(2)将日均收看该体育项目不低于![]() 分钟的观众称为“超级体育迷”,已知“超级体育述”中有
分钟的观众称为“超级体育迷”,已知“超级体育述”中有![]() 名女性,若从“超级体育述”中任意选取
名女性,若从“超级体育述”中任意选取![]() 人,求至少有
人,求至少有![]() 名女性观众的概率.
名女性观众的概率.
附: 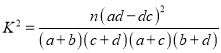 ,
,
|
|
|
|
|
|
|
|
|
|