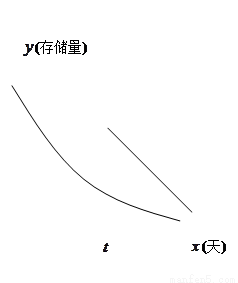题目内容
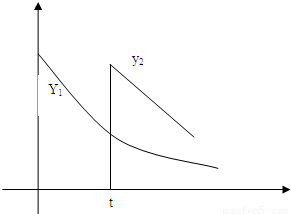 心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x 天后的存留量
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x 天后的存留量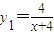 ;若在t(t>0)天时进行第一次复习,则此时这似乎存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为
;若在t(t>0)天时进行第一次复习,则此时这似乎存留量比未复习情况下增加一倍(复习的时间忽略不计),其后存留量y2随时间变化的曲线恰好为直线的一部分,其斜率为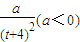 ,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”
,存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时刻为“二次复习最佳时机点”(1)若a=-1,t=5,求“二次复习最佳时机点”;
(2)若出现了“二次复习最佳时机点”,求a的取值范围.
【答案】分析:(1)t天时进行第一次复习后的存留量是过点(t, ),斜率为k=
),斜率为k= 的直线,方程为
的直线,方程为 ,不复习时x 天后的存留量为
,不复习时x 天后的存留量为 ,所以第一次复习后的存留量与不复习的存留量的差为y=y2-y1;把a=-1,t=5代入,整理可得所求.
,所以第一次复习后的存留量与不复习的存留量的差为y=y2-y1;把a=-1,t=5代入,整理可得所求.
(2)知识留存量函数y= +
+ -
- (其中t>4,且t、a是常数,x是自变量),当y取最大值时,求出对应的t、a取值范围.
(其中t>4,且t、a是常数,x是自变量),当y取最大值时,求出对应的t、a取值范围.
解答:解:(1)设第一次复习后的存留量与不复习的存留量之差为y,
由题意知, ,
,
所以, ;
;
当a=-1,t=5时, =
= ≤
≤ =
= ,
,
当且仅当x=14时取等号,
所以“二次复习最佳时机点”为第14天.
(2)知识留存量函数 =
=
≤ ,
,
当且仅当 时取等号,
时取等号,
由题意 ,所以-4<a<0.
,所以-4<a<0.
点评:本题考查了含有字母参数的函数类型的应用,题目中构造条件,利用基本不等式a+b≥2 (a>0,b>0)求最值,有些困难,属于较难题目.
(a>0,b>0)求最值,有些困难,属于较难题目.
 ),斜率为k=
),斜率为k= 的直线,方程为
的直线,方程为 ,不复习时x 天后的存留量为
,不复习时x 天后的存留量为 ,所以第一次复习后的存留量与不复习的存留量的差为y=y2-y1;把a=-1,t=5代入,整理可得所求.
,所以第一次复习后的存留量与不复习的存留量的差为y=y2-y1;把a=-1,t=5代入,整理可得所求.(2)知识留存量函数y=
 +
+ -
- (其中t>4,且t、a是常数,x是自变量),当y取最大值时,求出对应的t、a取值范围.
(其中t>4,且t、a是常数,x是自变量),当y取最大值时,求出对应的t、a取值范围.解答:解:(1)设第一次复习后的存留量与不复习的存留量之差为y,
由题意知,
 ,
,所以,
 ;
;当a=-1,t=5时,
 =
= ≤
≤ =
= ,
,当且仅当x=14时取等号,
所以“二次复习最佳时机点”为第14天.
(2)知识留存量函数
 =
=
≤
 ,
,当且仅当
 时取等号,
时取等号,由题意
 ,所以-4<a<0.
,所以-4<a<0.点评:本题考查了含有字母参数的函数类型的应用,题目中构造条件,利用基本不等式a+b≥2
 (a>0,b>0)求最值,有些困难,属于较难题目.
(a>0,b>0)求最值,有些困难,属于较难题目. 
练习册系列答案
相关题目
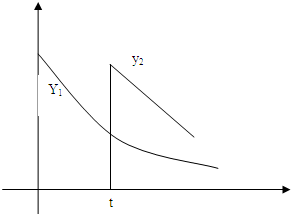 心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量
心理学家研究某位学生的学习情况发现:若这位学生刚学完的知识存留量为1,则x天后的存留量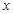 天后的存留量
天后的存留量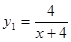 ;若在
;若在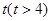 天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量
天时进行第一次复习,则此时知识存留量比未复习情况下增加一倍(复习时间忽略不计),其后存储量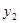 随时间变化的曲线恰为直线的一部分,其斜率为
随时间变化的曲线恰为直线的一部分,其斜率为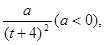 存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.
存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时,则称此时此刻为“二次复习最佳时机点”.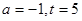 ,求“二次最佳时机点”;
,求“二次最佳时机点”;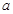 的取值范围.
的取值范围.