题目内容
已知函数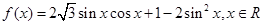 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数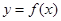 的图像上各点的纵坐标保持不变,横坐标缩短到原来的
的图像上各点的纵坐标保持不变,横坐标缩短到原来的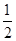 ,把所得到的图像再向左平移
,把所得到的图像再向左平移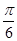 单位,得到的函数
单位,得到的函数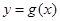 的图像,求函数
的图像,求函数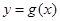 在区间
在区间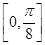 上的最小值.
上的最小值.
(1)函数f(x)的最小正周期为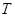 =
= .
.
f(x)的单调递增区间为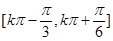 ,
, 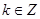 .
.
(2)当x = 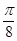 时,
时,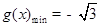 .
.
解析试题分析:(1)因为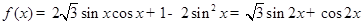 =
=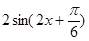 ,
,
函数f(x)的最小正周期为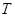 =
= .
.
由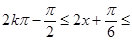
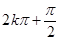 ,
,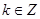 ,
,
得f(x)的单调递增区间为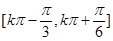 ,
, 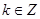 .
.
(2)根据条件得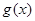 =
=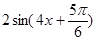 ,当
,当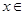
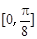 时,
时,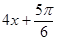

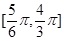 ,
,
所以当x = 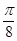 时,
时,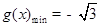 .
.
考点:本题主要考查三角函数的和差倍半公式的应用,三角函数的图象和性质,正弦型函数的图象变换。
点评:典型题,涉及三角函数的考题,往往需要先利用三角函数公式,将函数“化一”,以便进一步研究函数的性质。关于复合函数的单调区间的确定,遵循“内外层函数,同增异减”。本题(3)涉及角的范围,极易出错,应特别注意。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
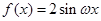 ·
·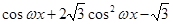 (其中
(其中 >o),且函数
>o),且函数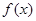 的最小正周期为
的最小正周期为
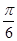 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.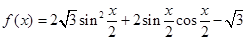 ,
,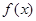 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
.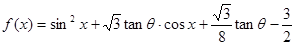 ,其中
,其中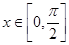 ,
,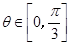
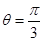 时,求
时,求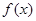 的最大值及相应的
的最大值及相应的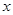 的值;
的值; ,使得函数
,使得函数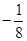 ?若存在,求出对应的
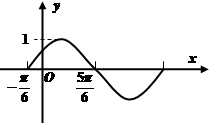
?若存在,求出对应的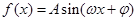 的图像如图所示,其中
的图像如图所示,其中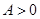 ,
,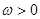 ,
,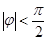 .
.
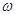 、
、 的值;
的值; 经过平移变换可否得到函数
经过平移变换可否得到函数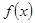 的图像?若能,平移的最短距离是多少个单位?否则,说明理由.
的图像?若能,平移的最短距离是多少个单位?否则,说明理由. .
.  的值.
的值. 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图
,其图象如图
 在
在 的表达式;
的表达式; 的解.
的解.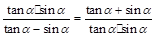 .
.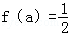 的a的值,并对此时的a值求y的最大值.
的a的值,并对此时的a值求y的最大值.